题目内容
如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是 .
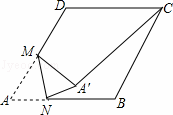
 ﹣1 解:如图所示:∵MA′是定值,A′C长度取最小值时,即A′在MC上时,
﹣1 解:如图所示:∵MA′是定值,A′C长度取最小值时,即A′在MC上时,
过点M作MF⊥DC于点F,
∵在边长为2的菱形ABCD中,∠A=60°,M为AD中点,
∴2MD=AD=CD=2,∠FDM=60°,
∴∠FMD=30°,
∴FD= MD=
MD= ,
,
∴FM=DM×cos30°= ,
,
∴MC= =
= ,
,
∴A′C=MC﹣MA′= ﹣1.
﹣1.
故答案为: ﹣1.
﹣1.


练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
某林业部门要考 查某种幼树在一定条件的移植成活率.在同样条件下,大量地对这种幼树进行移植,并统计成活情况,计算成活的频率.如下表:
查某种幼树在一定条件的移植成活率.在同样条件下,大量地对这种幼树进行移植,并统计成活情况,计算成活的频率.如下表:
| 移植总数(n) | 成活数(m) | 成活的频率 |
| 10 | 8 | 0.80 |
| 50 | 47 | 0.94 |
| 270 | 235 | 0.870 |
| 400 | 369 | 0.923 |
| 750 | 662 | 0.883 |
| 1500 | 1335 | 0.89 |
| 3500 | 3203 | 0.915 |
| 7000 | 6335 | 0.905 |
| 9000 | 8073 | 0.897 |
| 14000 | 12628 | 0.902 |
所以可以估计这种幼树移植成活的概率为
(A)0.1 (B)0.2 (C)0.8 (D)0.9

 辆)依次为11,13,15,19,x.若这五个数的平均数为16,则x=
辆)依次为11,13,15,19,x.若这五个数的平均数为16,则x= 
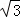 MN.
MN.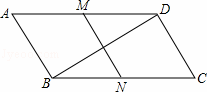

 过点(0,0),(1,3),求抛物线的解析式,并求出抛物线的顶点坐标.
过点(0,0),(1,3),求抛物线的解析式,并求出抛物线的顶点坐标.