题目内容
20.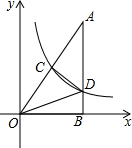 如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=$\frac{k}{x}$(x>0)经过斜边OA的中点C,与另一直角边交于点D,若S△OCD=12,则k的值为16.
如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=$\frac{k}{x}$(x>0)经过斜边OA的中点C,与另一直角边交于点D,若S△OCD=12,则k的值为16.
分析 作CE⊥OB于E,如图,根据反比例函数的比例系数k的几何意义得到S△OCE=S△BOD=$\frac{1}{2}$k,再根据三角形面积公式得到S△ACD=12,且OC=$\frac{1}{2}$OA,则S△OAB=24+$\frac{1}{2}$k,然后证明△OCE∽△OAQB,利用相似三角形的性质得到$\frac{{S}_{△OCE}}{{S}_{△OAB}}$=($\frac{OC}{OA}$)2,即$\frac{\frac{1}{2}k}{24+\frac{1}{2}k}$=$\frac{1}{4}$,再利用比例性质计算k的值.
解答 解: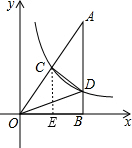 作CE⊥OB于E,如图,
作CE⊥OB于E,如图,
∵点C、D在双曲线y=$\frac{k}{x}$(x>0)上,
∴S△OCE=S△BOD=$\frac{1}{2}$k,
∵点C为OA的中点,S△OCD=12,
∴S△ACD=12,OC=$\frac{1}{2}$OA,
∴S△OAB=24+$\frac{1}{2}$k,
∵CE∥AB,
∴△OCE∽△OAQB,
∴$\frac{{S}_{△OCE}}{{S}_{△OAB}}$=($\frac{OC}{OA}$)2,即$\frac{\frac{1}{2}k}{24+\frac{1}{2}k}$=$\frac{1}{4}$,
∴k=16.
故答案为16.
点评 本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.在平面直角坐标系中,函数y=-x-1的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
12.四张质地、大小相同的卡片上,分别画上如图所示的四个图形,在看不到图形的情况下从中任意抽出一张卡片,则抽出的卡片上的图形是中心对称图形的概率为( )
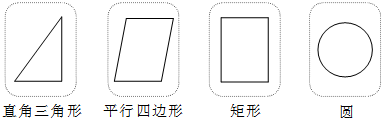

| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | 1 |
9.下列二次根式中,能与$\sqrt{2}$合并的是( )
| A. | $\sqrt{20}$ | B. | $\sqrt{12}$ | C. | $\sqrt{8}$ | D. | $\sqrt{4}$ |
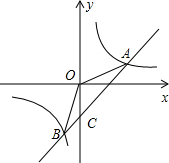 如图,已知一次函数y=kx+b的图象和反比例函数$y=\frac{3}{x}$的图象相交于A(3,m),B(n,-3)两点
如图,已知一次函数y=kx+b的图象和反比例函数$y=\frac{3}{x}$的图象相交于A(3,m),B(n,-3)两点