题目内容
如图,设P为 在第一象限的图象上的任一点,点P关于y轴的对称点为P′,连接P′P、P′O、OP.
在第一象限的图象上的任一点,点P关于y轴的对称点为P′,连接P′P、P′O、OP.
(1)说明△POP′的面积永远为定值4.
(2)当P点移动到P1(x1,y1),点P1关于y轴的对称点为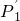 ,使△
,使△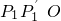 为等边三角形时,求OP1所在直线的解析式;
为等边三角形时,求OP1所在直线的解析式;
(3)当P点移动到P2(x2,y2),点P2关于y轴的对称点为 ,且y2=
,且y2=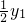 时,求梯形P1
时,求梯形P1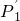
 P2的面积.
P2的面积.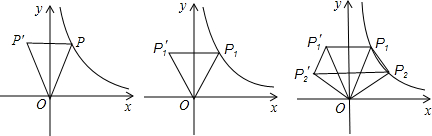
解:(1)过P点作PH⊥x轴,如图,设P点坐标为(x,y),
∵y= ,
,
∴xy=4,
∴S△OPH= xy=2,
xy=2,
∵点P关于x轴的对称点为P′,
∴S△P′PO=2S△OPH=4,
即△POP′的面积永远为定值4;
(2)过P1作P1A⊥x轴于A,如图,
∵点P1关于x轴的对称点为P1′,△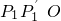 为等边三角形,
为等边三角形,
∴OP1与y轴的夹角为30°,
∴∠AOP1=60°,
∴P1A= OA,
OA,
设P1的坐标为(x1, x1),直线OP1的解析式为y=kx,
x1),直线OP1的解析式为y=kx,
把P1的坐标代入可解得k= ,
,
∴OP1所在直线的解析式为:y= x;
x;

(3)过P1作P1B⊥x轴于B,交P2P2′于C,如图,
∵P1(x1,y1)、P2(x2,y2)都在y= 上,且y2=
上,且y2=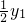 ,
,
∴x1•y1=4,x2•y2=4,x2=2x1,
∴P1C=y1-y2= y1,
y1,
∴梯形P1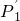
 P2的面积=
P2的面积= (P1P1′+P2P2′)•P1C
(P1P1′+P2P2′)•P1C
= (2x1+2x2)(y1-y2)
(2x1+2x2)(y1-y2)
= •6x1•
•6x1• y1
y1
= •x1•y1
•x1•y1
= ×4
×4
=6.
分析:(1)过P点作PH⊥x轴,如图,设P点坐标为(x,y),易得S△OPH= xy=2,根据对称的性质得到S△P′PO=2S△OPH=4;
xy=2,根据对称的性质得到S△P′PO=2S△OPH=4;
(2)过P1作P1A⊥x轴于A,由点P1关于x轴的对称点为P1′,△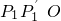 为等边三角形,得OP1与y轴的夹角为30°,则∠AOP1=60°,利用含30度的直角三角形三边的关系得到P1A=
为等边三角形,得OP1与y轴的夹角为30°,则∠AOP1=60°,利用含30度的直角三角形三边的关系得到P1A= OA,这样可设P1的坐标为(x1,
OA,这样可设P1的坐标为(x1, x1),直线OP1的解析式为y=kx,然后把P1的坐标代入可解得k=
x1),直线OP1的解析式为y=kx,然后把P1的坐标代入可解得k= ,从而确定OP1所在直线的解析式;
,从而确定OP1所在直线的解析式;
(3)过P1作P1A⊥x轴于B,交P2P2′于C,根据P1(x1,y1)、P2(x2,y2)都在y= 上,且y2=
上,且y2=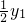 ,可得到x1•y1=4,x2•y2=4,x2=2x1,则P1C=y1-y2=
,可得到x1•y1=4,x2•y2=4,x2=2x1,则P1C=y1-y2= y1,利用梯形的面积公式得到梯形P1
y1,利用梯形的面积公式得到梯形P1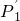
 P2的面积=
P2的面积= (P1P1′+P2P2′)•P1C=
(P1P1′+P2P2′)•P1C= (2x1+2x2)(y1-y2)=
(2x1+2x2)(y1-y2)= •6x1•
•6x1• y1,把x1•y1=4代入计算即可.
y1,把x1•y1=4代入计算即可.
点评:本题考查了反比例函数的综合题:点在反比例函数图形上,点的坐标满足其解析式;点的坐标与线段之间的关系;对称和等边三角形的性质以及含30度的直角三角形三边的关系.
∵y=
 ,
,∴xy=4,
∴S△OPH=
 xy=2,
xy=2,∵点P关于x轴的对称点为P′,
∴S△P′PO=2S△OPH=4,
即△POP′的面积永远为定值4;
(2)过P1作P1A⊥x轴于A,如图,
∵点P1关于x轴的对称点为P1′,△
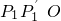 为等边三角形,
为等边三角形,∴OP1与y轴的夹角为30°,
∴∠AOP1=60°,
∴P1A=
 OA,
OA,设P1的坐标为(x1,
 x1),直线OP1的解析式为y=kx,
x1),直线OP1的解析式为y=kx,把P1的坐标代入可解得k=
 ,
,∴OP1所在直线的解析式为:y=
 x;
x;
(3)过P1作P1B⊥x轴于B,交P2P2′于C,如图,
∵P1(x1,y1)、P2(x2,y2)都在y=
 上,且y2=
上,且y2=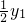 ,
,∴x1•y1=4,x2•y2=4,x2=2x1,
∴P1C=y1-y2=
 y1,
y1,∴梯形P1
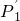
 P2的面积=
P2的面积= (P1P1′+P2P2′)•P1C
(P1P1′+P2P2′)•P1C=
 (2x1+2x2)(y1-y2)
(2x1+2x2)(y1-y2)=
 •6x1•
•6x1• y1
y1=
 •x1•y1
•x1•y1=
 ×4
×4=6.
分析:(1)过P点作PH⊥x轴,如图,设P点坐标为(x,y),易得S△OPH=
 xy=2,根据对称的性质得到S△P′PO=2S△OPH=4;
xy=2,根据对称的性质得到S△P′PO=2S△OPH=4;(2)过P1作P1A⊥x轴于A,由点P1关于x轴的对称点为P1′,△
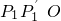 为等边三角形,得OP1与y轴的夹角为30°,则∠AOP1=60°,利用含30度的直角三角形三边的关系得到P1A=
为等边三角形,得OP1与y轴的夹角为30°,则∠AOP1=60°,利用含30度的直角三角形三边的关系得到P1A= OA,这样可设P1的坐标为(x1,
OA,这样可设P1的坐标为(x1, x1),直线OP1的解析式为y=kx,然后把P1的坐标代入可解得k=
x1),直线OP1的解析式为y=kx,然后把P1的坐标代入可解得k= ,从而确定OP1所在直线的解析式;
,从而确定OP1所在直线的解析式;(3)过P1作P1A⊥x轴于B,交P2P2′于C,根据P1(x1,y1)、P2(x2,y2)都在y=
 上,且y2=
上,且y2=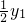 ,可得到x1•y1=4,x2•y2=4,x2=2x1,则P1C=y1-y2=
,可得到x1•y1=4,x2•y2=4,x2=2x1,则P1C=y1-y2= y1,利用梯形的面积公式得到梯形P1
y1,利用梯形的面积公式得到梯形P1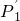
 P2的面积=
P2的面积= (P1P1′+P2P2′)•P1C=
(P1P1′+P2P2′)•P1C= (2x1+2x2)(y1-y2)=
(2x1+2x2)(y1-y2)= •6x1•
•6x1• y1,把x1•y1=4代入计算即可.
y1,把x1•y1=4代入计算即可.点评:本题考查了反比例函数的综合题:点在反比例函数图形上,点的坐标满足其解析式;点的坐标与线段之间的关系;对称和等边三角形的性质以及含30度的直角三角形三边的关系.

练习册系列答案
相关题目
 行于x轴,交y轴于点M,交过点B垂直于x轴的直线于点N.
行于x轴,交y轴于点M,交过点B垂直于x轴的直线于点N.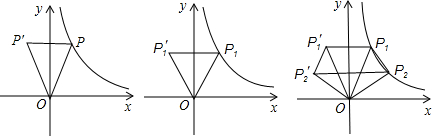
 在第一象限的图象上的任一点,点P关于y轴的对称点为P′,连接P′P、P′O、OP.
在第一象限的图象上的任一点,点P关于y轴的对称点为P′,连接P′P、P′O、OP.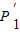 ,使△
,使△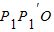 为等边三角形时,求OP1所在直线的解析式;
为等边三角形时,求OP1所在直线的解析式; ,且y2=
,且y2= 时,求梯形P1
时,求梯形P1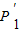
 P2的面积.
P2的面积.