题目内容
如图,抛物线y=-2x2+x+1交y轴于点A,交x轴正半轴于点B.P为线段AB上一动点,作直线PC⊥PO,交过点B垂直于x轴的直线于点C.过P点作直线MN平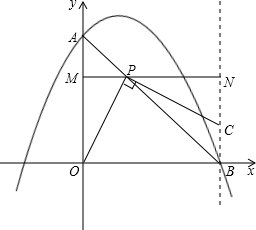 行于x轴,交y轴于点M,交过点B垂直于x轴的直线于点N.
行于x轴,交y轴于点M,交过点B垂直于x轴的直线于点N.(1)求线段AB长;
(2)证明:OP=PC;
(3)当点P在第一象限时,设AP长为m,△OBC的面积为S,请求出S与m间的函数关系式,并写出自变量m的取值范围;
(4)当点P在线段AB上移动时,点C也随之在直线x=1上移动,△PBC是否可能成为等腰三角形?如果可能,求出所有能使△PBC成为等腰三角形的点P的坐标;如果不可能,请说明理由.
分析:(1)根据抛物线的解析式,易求得A、B的坐标,利用勾股定理即可求得AB的长.
(2)首先根据A、B的坐标,求出直线AB的解析式,设出点P的横坐标,利用直线AB的解析式,即可表示出P点的纵坐标,由此可得到MP、OM、PN的长,从而证得OM=PN,而∠OPC=90°,则∠OPM、∠PCN同为∠CPN的余角,再加上一组直角,即可由AAS判定△OPM≌△PCN,由此得证.
(3)由(2)的全等三角形知PM=CN,由此可求得BC的表达式,OB的长易求得,根据三角形的面积公式即可得到S、m的函数关系式.(需注意的是,自变量的取值范围会影响到PM的表达式,因此要分类讨论)
(4)此题应分三种情况讨论:
①P为等腰三角形的顶角顶点,由于∠PBN=45°,若PC=PB,那么CP⊥PB,显然不符合题意;
②C为等腰三角形的顶角顶点,此时PC=BC,由于△OAB是等腰直角三角形,因此P、A重合时,△PCB也是等腰直角三角形,故A点符合点P的要求;
③B为等腰三角形的顶角顶点,此时PB=BC;当C点在第一象限时,显然不存在这样的P点,故此时C点必在第四象限,首先设出点P的坐标,表示出AP、PB、BC的长,根据所得等量关系,即可得到点P的坐标.
(2)首先根据A、B的坐标,求出直线AB的解析式,设出点P的横坐标,利用直线AB的解析式,即可表示出P点的纵坐标,由此可得到MP、OM、PN的长,从而证得OM=PN,而∠OPC=90°,则∠OPM、∠PCN同为∠CPN的余角,再加上一组直角,即可由AAS判定△OPM≌△PCN,由此得证.
(3)由(2)的全等三角形知PM=CN,由此可求得BC的表达式,OB的长易求得,根据三角形的面积公式即可得到S、m的函数关系式.(需注意的是,自变量的取值范围会影响到PM的表达式,因此要分类讨论)
(4)此题应分三种情况讨论:
①P为等腰三角形的顶角顶点,由于∠PBN=45°,若PC=PB,那么CP⊥PB,显然不符合题意;
②C为等腰三角形的顶角顶点,此时PC=BC,由于△OAB是等腰直角三角形,因此P、A重合时,△PCB也是等腰直角三角形,故A点符合点P的要求;
③B为等腰三角形的顶角顶点,此时PB=BC;当C点在第一象限时,显然不存在这样的P点,故此时C点必在第四象限,首先设出点P的坐标,表示出AP、PB、BC的长,根据所得等量关系,即可得到点P的坐标.
解答:解:(1)抛物线y=-2x2+x+1中,令x=0,得y=1,令y=0,得x=-
,x=1;
故A(0,1),B(1,0);
∴AB=
.(2分)
(2)∵A(0,1),B(1,0),
∴直线AB:y=-x+1;
设P(a,-a+1),则有:
PM=a,OM=1-a,PN=MN-PM=1-a,
故OM=PN;
∵∠OPC=90°,则∠OPM+∠CPN=∠CPN+∠PCN=90°,
∴∠OPM=∠PCN;
又∵∠OMP=∠CPN=90°,OM=PN,
∴△OPM≌△PCN,
∴OP=CP.(5分)
(3)易知OA=OB=1,则∠OBA=∠OAB=45°;
若AP=m,则PM=AM=CN=
m,OM=BN=1-
m,
①当0<m<
时,BC=BN-NC=1-
-
=1-
m,
故S=
;(7分)
②当
<m<
时,BC=CN-BN=
-(1-
)=
m-1,
故S=-
.(9分)
(4)假设存在符合条件的P点;
①△PCB以P为顶角顶点,此时点C位于第一象限;
由于∠PBN=45°,若PC=PB,则∠CPB=90°,显然不合题意;
②△PCB以C为顶角顶点;
由于△OAB是等腰直角三角形,当P、A重合时,△PCB也是等腰直角三角形,
故A点符合P点的要求,即P(0,1);
③△PBC以B为顶角顶点;
当C点在第一象限时,PB>BC,若PB=BC,则C点必在第四象限;
设P(a,1-a),则AP=
a,PB=
(1-a),BC=CN-BN=a-(1-a)=2a-1;
若PB=BC,则2a-1=
-
a,
解得a=
,
故P(
,1-
);
综上所述,存在符合条件的P点,且坐标为P(0,1)或(
,1-
).(12分)
| 1 |
| 2 |
故A(0,1),B(1,0);
∴AB=
| 2 |
(2)∵A(0,1),B(1,0),
∴直线AB:y=-x+1;
设P(a,-a+1),则有:
PM=a,OM=1-a,PN=MN-PM=1-a,
故OM=PN;
∵∠OPC=90°,则∠OPM+∠CPN=∠CPN+∠PCN=90°,
∴∠OPM=∠PCN;
又∵∠OMP=∠CPN=90°,OM=PN,
∴△OPM≌△PCN,
∴OP=CP.(5分)
(3)易知OA=OB=1,则∠OBA=∠OAB=45°;
若AP=m,则PM=AM=CN=
| ||
| 2 |
| ||
| 2 |
①当0<m<
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
故S=
1-
| ||
| 2 |
②当
| ||
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
故S=-
1-
| ||
| 2 |
(4)假设存在符合条件的P点;
①△PCB以P为顶角顶点,此时点C位于第一象限;
由于∠PBN=45°,若PC=PB,则∠CPB=90°,显然不合题意;
②△PCB以C为顶角顶点;
由于△OAB是等腰直角三角形,当P、A重合时,△PCB也是等腰直角三角形,
故A点符合P点的要求,即P(0,1);
③△PBC以B为顶角顶点;
当C点在第一象限时,PB>BC,若PB=BC,则C点必在第四象限;
设P(a,1-a),则AP=
| 2 |
| 2 |
若PB=BC,则2a-1=
| 2 |
| 2 |
解得a=
| ||
| 2 |
故P(
| ||
| 2 |
| ||
| 2 |
综上所述,存在符合条件的P点,且坐标为P(0,1)或(
| ||
| 2 |
| ||
| 2 |
点评:此题主要考查了抛物线与坐标轴交点坐标的求法、全等三角形的判定、等腰直角三角形的性质、等腰三角形的构成条件等知识.(4)题中,由于等腰三角形的腰和底不确定,一定要分类讨论,以免漏解.

练习册系列答案
相关题目
 如图,抛物线y=ax2+bx+c(a≠0)与x轴两交点是A(-1,0),B(3,0),则如图可知y<0时,x的取值范围是( )
如图,抛物线y=ax2+bx+c(a≠0)与x轴两交点是A(-1,0),B(3,0),则如图可知y<0时,x的取值范围是( )| A、-1<x<3 | B、3<x<-1 | C、x>-1或x<3 | D、x<-1或x>3 |
 26、已知:如图,抛物线C1,C2关于x轴对称;抛物线C1,C3关于y轴对称.抛物线C1,C2,C3与x轴相交于A、B、C、D四点;与y相交于E、F两点;H、G、M分别为抛物线C1,C2,C3的顶点.HN垂直于x轴,垂足为N,且|OE|>|HN|,|AB|≠|HG|
26、已知:如图,抛物线C1,C2关于x轴对称;抛物线C1,C3关于y轴对称.抛物线C1,C2,C3与x轴相交于A、B、C、D四点;与y相交于E、F两点;H、G、M分别为抛物线C1,C2,C3的顶点.HN垂直于x轴,垂足为N,且|OE|>|HN|,|AB|≠|HG| 如图,抛物线交x轴于点A(-2,0),点B(4,0),交y轴于点C(0,4).
如图,抛物线交x轴于点A(-2,0),点B(4,0),交y轴于点C(0,4). 以P为圆心的圆经过点A,并且与直线BM相切?若存在,求出点P的坐标;若不存在,请说明理由.
以P为圆心的圆经过点A,并且与直线BM相切?若存在,求出点P的坐标;若不存在,请说明理由. .点C是点A关于点B的对称点,点F是线段BC的中点,直线l过点F且与y轴平行.直线y=-x+m过点C,交y轴于D点.
.点C是点A关于点B的对称点,点F是线段BC的中点,直线l过点F且与y轴平行.直线y=-x+m过点C,交y轴于D点.