题目内容
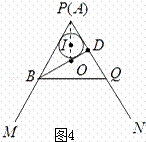
已知:∠MAN=60°,点B在射线AM上,AB=4(如图).P为直线AN上一动点,以BP为边作等边三角形BPQ(点B,P,Q按顺时针排列),O是△BPQ的外心.
(1)当点P在射线AN上运动时,求证:点O在∠MAN的平分线上;
(2)当点P在射线AN上运动(点P与点A不重合)时,AO与BP交于点C,设AP=x,AC•AO=y,求y关于x的函数解析式,并写出函数的定义域;
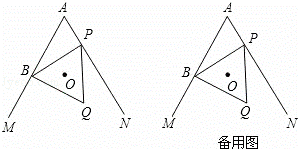 (3)若点D在射线AN上,AD=2,圆I为△ABD的内切圆.当△BPQ的边BP或BQ与圆I相切时,请直接写出点A与点O的距离.
(3)若点D在射线AN上,AD=2,圆I为△ABD的内切圆.当△BPQ的边BP或BQ与圆I相切时,请直接写出点A与点O的距离.
 (1)证明:如图1,连接OB,OP.
(1)证明:如图1,连接OB,OP.
∵O是等边三角形BPQ的外心,
∴圆心角∠BOP=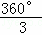 =120°.
=120°.
当∠MAN=60°,不垂直于AM时,作OT⊥AN,则OB=OP.
由∠HOT+∠A+∠AHO+∠ATO=360°,且∠A=60°,∠AHO=∠ATO=90°,
∴∠HOT=120度.
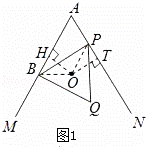 ∴∠BOH=∠POT.
∴∠BOH=∠POT.
∴Rt△BOH≌Rt△POT.
∴OH=OT.
∴点O在∠MAN的平分线上.
当OB⊥AM时,∠APO=360°﹣∠A﹣∠BOP﹣∠OBA=90°.
即OP⊥AN,
∴点O在圆I的平分线上.
综上所述,当点P在射线AN上运动时,点O在∠MAN的平分线上.
(2)解:如图2,
∵AO平分∠MAN,且∠MAN=60°,
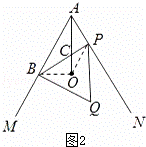 ∴∠BAO=∠PAO=30°.
∴∠BAO=∠PAO=30°.
由(1)知,OB=OP,∠BOP=120°,
∴∠CBO=30°,
∴∠CBO=∠PAC.
∵∠BCO=∠PCA,
∴∠AOB=∠APC.
∴△ABO∽△ACP.
∴ .
.
∴AC•AO=AB•AP.
∴y=4x.
定义域为:x>0.
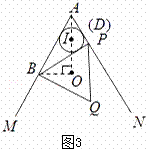
(3)解:①如图3,当BP与圆I相切时,AO=2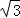 ;
;
②如图4,当BP与圆I相切时,AO=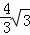 ;
;
③如图5,当BQ与圆I相切时,AO=0.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ( )
( )
 .
.

 ,则扇形的圆心角为 .
,则扇形的圆心角为 .