题目内容
17.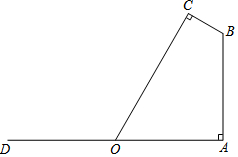 如图,若要在宽AD为20米的城南大道两边安装路灯,路灯的灯臂BC长2米,且与灯柱AB成120°角,路灯采用圆锥形灯罩,灯罩的轴线CO与灯臂BC垂直,当灯罩的轴线CO通过公路路面的中心线时照明效果最好,此时,路灯的灯柱AB高应该设计为多少米(结果保留根号)?
如图,若要在宽AD为20米的城南大道两边安装路灯,路灯的灯臂BC长2米,且与灯柱AB成120°角,路灯采用圆锥形灯罩,灯罩的轴线CO与灯臂BC垂直,当灯罩的轴线CO通过公路路面的中心线时照明效果最好,此时,路灯的灯柱AB高应该设计为多少米(结果保留根号)?
分析 延长OC,AB交于点P,△PCB∽△PAO,根据相似三角形对应边比例相等的性质即可解题.
解答 解:如图,延长OC,AB交于点P.
∵∠ABC=120°,
∴∠PBC=60°,
∵∠OCB=∠A=90°,
∴∠P=30°,
∵AD=20米,
∴OA=$\frac{1}{2}$AD=10米,
∵BC=2米,
∴在Rt△CPB中,PC=BC•tan60°=2$\sqrt{3}$米,PB=2BC=4米,
∵∠P=∠P,∠PCB=∠A=90°,
∴△PCB∽△PAO,
∴$\frac{PC}{PA}=\frac{BC}{OA}$,
∴PA=$\frac{PC•OA}{BC}$=$\frac{{2\sqrt{3}×10}}{2}$=10$\sqrt{3}$米,
∴AB=PA-PB=(10$\sqrt{3}$-4)米.
答:路灯的灯柱AB高应该设计为(10$\sqrt{3}$-4)米.
点评 本题考查了通过作辅助线构建直角三角形的能力,考查了相似三角形的判定和性质,本题中求证△PCB∽△PAO是解题的关键.

练习册系列答案
相关题目
8.为有效开展“阳光体育”活动,某校计划购买篮球和足球共50个,购买资金不超过3000元.若每个篮球80元,每个足球50元,则篮球最多可购买( )
| A. | 16个 | B. | 17个 | C. | 33个 | D. | 34个 |
2.2017的相反数是( )
| A. | -2017 | B. | 2017 | C. | -$\frac{1}{2017}$ | D. | $\frac{1}{2017}$ |
9.若分式$\frac{{x}^{2}-1}{x-1}$的值为0,则x的值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | ±1 |
6.若关于x的一元二次方程kx2-2x-1=0有两个不相等的实数根,则实数k的取值范围是( )
| A. | k>-1 | B. | k>-1且k≠0 | C. | k<-1 | D. | k<-1或k=0 |
 如图,BC∥EF,AC∥DF,添加一个条件AB=DE或BC=EF或AC=DF或AD=BE(只需添加一个即可),使得△ABC≌△DEF.
如图,BC∥EF,AC∥DF,添加一个条件AB=DE或BC=EF或AC=DF或AD=BE(只需添加一个即可),使得△ABC≌△DEF. 如图,P、Q分别是⊙O的内接正五边形的边AB、BC上的点,BP=CQ,则∠POQ=72°.
如图,P、Q分别是⊙O的内接正五边形的边AB、BC上的点,BP=CQ,则∠POQ=72°.