题目内容
【题目】如图是规格为![]() 的正方形网格,请在所给网格中按下列要求操作:
的正方形网格,请在所给网格中按下列要求操作:
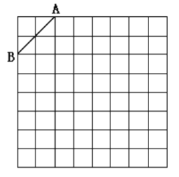
(1)请在网格中建立平面直角坐标系,使点![]() 坐标为
坐标为![]() ,
,![]() 点坐标为
点坐标为![]() ;
;
(2)在第二象限内的格点上画一点![]() ,使点
,使点![]() 与线段
与线段![]() 组成一个以
组成一个以![]() 为底的等腰三角形,且腰长是无理数, 则
为底的等腰三角形,且腰长是无理数, 则![]() 点坐标是________,
点坐标是________,![]() 的周长是_________(结果保留根号);
的周长是_________(结果保留根号);
(3)画出![]() 以点
以点![]() 为旋转中心、旋转
为旋转中心、旋转![]() 后的
后的![]() ,连结
,连结![]() 和
和![]() ,试说出四边形
,试说出四边形![]() 是何特殊四边形, 并说明理由.
是何特殊四边形, 并说明理由.
【答案】(1)答案见解析;(2)![]() ,
,![]() ;(3)作图见解析;矩形,理由见解析.
;(3)作图见解析;矩形,理由见解析.
【解析】
(1)根据题意画出平面直角坐标系即可;
(2)找出线段AB的垂直平分线,与格点相交于点C,满足腰长为无理数,则C点即为所求点,求出AC、BC,即可得出△ABC的周长;
(3)先画出图形,结合图形即可作出判断.
(1)如图所示:该平面直角坐标系为所求;
(2)如图所示:C为所求;
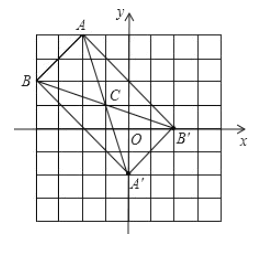
由坐标系可知:AC=BC=![]() ,AB=
,AB=![]()
△ABC的周长是:![]()
故答案为:![]() ,
,![]()
(3)如图所示:![]() 为所求
为所求
由旋转180°可知,BC=CB′,AC=CA′,
∴四边形ABA′B′是平行四边形,
又∵AA′=BB′![]() ,
,
∴四边形ABA′B′是矩形.

练习册系列答案
相关题目
【题目】已知二次函数![]() 的
的![]() 与
与![]() 的部分对应值如表:
的部分对应值如表:
|
|
|
|
|
|
|
|
|
|
|
|
下列结论:![]() 抛物线的开口向上;②抛物线的对称轴为直线
抛物线的开口向上;②抛物线的对称轴为直线![]() ;③当
;③当![]() 时,
时,![]() ;④抛物线与
;④抛物线与![]() 轴的两个交点间的距离是
轴的两个交点间的距离是![]() ;⑤若
;⑤若![]() 是抛物线上两点,则
是抛物线上两点,则![]() ,其中正确的个数是( )
,其中正确的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()