题目内容
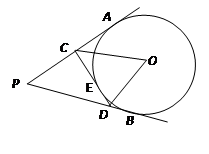
PA、PB是⊙O的切线，切点是A、B，∠APB=50°，过A作⊙O直径AC，连接CB，则∠PBC=________．
155°
分析：先画图，由切线的性质，求出∠AOB，再由外角的性质求得∠OBC，则∠PBC=∠OBC+∠PBO即可．
解答：
解：如图，连接OB，
∵PA、PB是⊙O的切线，∴∠PAO=∠PBO=90°，
∵∠APB=50°，∴∠AOB=130°，
∵∠AOB=∠C+∠OBC，∴∠OBC=
∠AOB=65°，
∴∠PBC=∠PBO+∠OBC=90°+65°=155°．
故答案为155°．
点评：本题考查了切线长定理、切线的性质和圆周角定理，解决这类问题常把它转化为三角形问题解决．
分析：先画图，由切线的性质，求出∠AOB，再由外角的性质求得∠OBC，则∠PBC=∠OBC+∠PBO即可．
解答：
解：如图，连接OB，∵PA、PB是⊙O的切线，∴∠PAO=∠PBO=90°，
∵∠APB=50°，∴∠AOB=130°，
∵∠AOB=∠C+∠OBC，∴∠OBC=
∠AOB=65°，∴∠PBC=∠PBO+∠OBC=90°+65°=155°．
故答案为155°．
点评：本题考查了切线长定理、切线的性质和圆周角定理，解决这类问题常把它转化为三角形问题解决．
练习册系列答案
百年学典课时学练测系列答案
相关题目
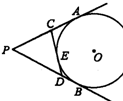
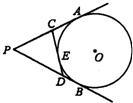7、如图，PA、PB是⊙O的两条切线，A、B是切点，CD切劣弧AB于点E，已知切线PA的长为6cm，则△PCD的周长为
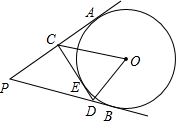如图，PA、PB是⊙O的切线，CD切⊙O于点E，△PCD的周长为12，∠APB=60°．求：
如图，PA、PB是⊙O的切线，点C在
