题目内容
现有A、B两枚均匀的小立方体（立方体的每个面上分别标有数字1、2、3、4、5、6），小明用掷A立方体朝上的数字为x，掷B立方体朝上的数字为y来确定点P（x，y），则小明各掷一次确定的点P落在已知抛物线y=-x2+4x+3上的概率是________．
分析：依据题意先用列表法或画树状图法分析所有等可能的出现结果，求得小明各掷一次确定的点P落在已知抛物线y=-x2+4x+3上的情况数，然后根据概率公式即可求出该事件的概率．
解答：列表得：（1，6）（2，6）（3，6）（4，6）（5，6）（6，6）（1，5）（2，5）（3，5）（4，5）（5，5）（6，5）（1，4）（2，4）（3，4）（4，4）（5，4）（6，4）（1，3）（2，3）（3，3）（4，3）（5，3）（6，3）（1，2）（2，2）（3，2）（4，2）（5，2）（6，2）（1，1）（2，1）（3，1）（4，1）（5，1）（6，1）∴一共有36种等可能的结果，
小明各掷一次确定的点P落在已知抛物线y=-x2+4x+3上的有（1，6），（3，6），（4，3）共3种，
∴小明各掷一次确定的点P落在已知抛物线y=-x2+4x+3上的概率是
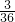=．故答案为：
．点评：本题考查的是用列表法或画树状图法求概率．列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
（课改）现有A、B两枚均匀的小立方体（立方体的每个面上分别标有数字1，2，3，4，5，6）．用小莉掷A立方体朝上的数字为x小明掷B立方体朝上的数字为y来确定点P（x，y），那么它们各掷一次所确定的点P落在已知抛物线y=-x2+4x上的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
现有A、B两枚均匀的小立方体（立方体的每个面上分别标有数字1，2，3，4，5，6）．用小莉掷A立方体朝上的数字为x、小明掷B立方体朝上的数字为y来确定点P（x，y），那么他们各掷一次所确定的点P落在双曲线y=
上的概率为（ ）
| 6 |
| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
现有A、B两枚均匀的小立方体骰子（立方体的每个面上分别标有数字1，2，3，4，5，6）．用小莉掷A立方体朝上的数字为x、小明掷B立方体朝上的数字为y来确定点P（x，y），那么它们各掷一次所确定的点P落在已知直线y=2x上的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
现有A、B两枚均匀的正方体骰子（六个面上分别标有数字1到6）．小明掷A正方体朝上的数字x，小亮掷B正方体朝上的数字y，分别作点P的横坐标和纵坐标，那么他们各掷一次所确定的点P（x，y）落在如图所示的矩形内（含边界）的概率是（ ）