题目内容
20、(1)如图,BD与CD分别平分∠ABC和∠ACB,已知∠BDC=130°,求∠A的度数.
(2)将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,求∠1的度数.
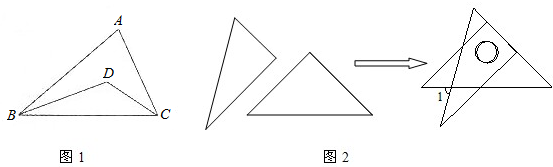
(2)将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,求∠1的度数.

分析:(1)先根据三角形的内角和求出∠DBC与∠DCB的度数的和,再根据角平分线的定义求出∠ABC与∠ACB的和,然后再根据三角形的内角和定理解答;
(2)根据三角形的内角和求出∠2=45°,再根据对顶角相等求出∠3=∠2,然后根据三角形的一个外角等于与它不相邻的两个内角的和计算即可.
(2)根据三角形的内角和求出∠2=45°,再根据对顶角相等求出∠3=∠2,然后根据三角形的一个外角等于与它不相邻的两个内角的和计算即可.
解答: 解:(1)在△BDC中,∵∠BDC=130°,
解:(1)在△BDC中,∵∠BDC=130°,
∴∠DBC+∠BCD=50°,…(2分)
又∵BD与CD分别平分∠ABC和∠ACB,
∴∠ABC+∠ACB=100°,…(4分)
∴∠A=180°-100°=80°;…(6分)
(2)如图,∠2=90°-45°=45°(直角三角形两锐角互余),
∴∠3=∠2=45°,
∴∠1=∠3+30°=45°+30°=75°.
故答案为:(1)80°,(2)75°.
 解:(1)在△BDC中,∵∠BDC=130°,
解:(1)在△BDC中,∵∠BDC=130°,∴∠DBC+∠BCD=50°,…(2分)
又∵BD与CD分别平分∠ABC和∠ACB,
∴∠ABC+∠ACB=100°,…(4分)
∴∠A=180°-100°=80°;…(6分)
(2)如图,∠2=90°-45°=45°(直角三角形两锐角互余),
∴∠3=∠2=45°,
∴∠1=∠3+30°=45°+30°=75°.
故答案为:(1)80°,(2)75°.
点评:本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,三角形的内角和定理,角平分线的定义,是基础题,比较简单.

练习册系列答案
相关题目
 如图,BD与CE相交于点A,已知,AB=6,AC=4,AD=3,且△ABC与△ADE相似,求AE的长.
如图,BD与CE相交于点A,已知,AB=6,AC=4,AD=3,且△ABC与△ADE相似,求AE的长. 11、如图,BD与CE分别是∠ABC和∠ACB的平分线,如果∠DBC=∠ECB,那么∠ABC=∠ACB吗?
11、如图,BD与CE分别是∠ABC和∠ACB的平分线,如果∠DBC=∠ECB,那么∠ABC=∠ACB吗? 如图,BD与CE分别是∠ABC和∠ACB的平分线,如果∠DBC=∠ECB,那么∠ABC
如图,BD与CE分别是∠ABC和∠ACB的平分线,如果∠DBC=∠ECB,那么∠ABC ∠ABC和∠ACB,已知∠BDC=
∠ABC和∠ACB,已知∠BDC= ,求∠A的度数。
,求∠A的度数。
