题目内容
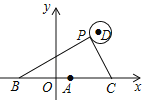
【题目】如图，一次函数y=kx+b（k＜0）与反比例函数
的图象相交于A、B两点，一次函数的图象与y轴相交于点C，已知点A（4，1）
（1）求反比例函数的解析式；
（2）连接OB（O是坐标原点），若△BOC的面积为3，求该一次函数的解析式．
【答案】（1）
；（2）
．
【解析】
（1）由点A的坐标结合反比例函数系数k的几何意义，即可求出m的值；
（2）设点B的坐标为（n，
），将一次函数解析式代入反比例函数解析式中，利用根与系数的关系可找出n、k的关系，由三角形的面积公式可表示出来b、n的关系，再由点A在一次函数图象上，可找出k、b的关系，联立3个等式为方程组，解方程组即可得出结论．
（1）∵点A（4，1）在反比例函数
的图象上，
∴m=4×1=4，
∴反比例函数的解析式为．
（2）∵点B在反比例函数的图象上，
∴设点B的坐标为（n，）．
将y=kx+b代入中，得：kx+b=
，
整理得：
，∴4n=
，即nk=﹣1①．
令y=kx+b中x=0，则y=b，
即点C的坐标为（0，b），
∴S△BOC=
bn=3，∴bn=6②．
∵点A（4，1）在一次函数y=kx+b的图象上，
∴1=4k+b③．
联立①②③成方程组，即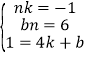
，解得：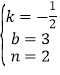
，
∴该一次函数的解析式为．
练习册系列答案
相关题目
