题目内容
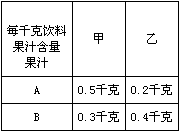
某饮料厂开发新产品,用A、B两种果汁原料按不同比例混合研制甲、乙两种新型饮料.现在分别有A、B果汁原料19千克、17.2千克,试生产两种饮料共50千克,每种饮料所需A、B果汁原料如下表:

(1)利用现有原料,工厂能否完成任务?若能,有几种生产方案?请你设计出来.(假设生产甲种饮料x千克)
(2)设甲种饮料每千克成本为4元,乙种饮料每千克成本为3元,这两种饮料的成本总额为y元,根据(1)的运算结果,确定当甲种饮料生产多少千克时,甲、乙两种饮料的成本总额y最小?
解:(1)假设生产甲种饮料x千克,那么生产乙种饮料(50-x)千克,
由题意得,生产甲饮料需要A,0.5xkg,乙需要A,0.2(50-x)kg,0.5x+0.2(50-x)≤19,
同理可得,甲,乙需要B饮料,0.3x+0.4(50-x)≤17.2,列出不等式组求出即可;
 ,
,
解:0.5x+0.2(50-x)≤19,
解得:x≤30,
解:0.3x+0.4(50-x)≤17.2,
解得:28≤x,
∴不等式组的解集是:28≤x≤30,
有3种生产方案,分别为①生产甲饮料28kg,乙原料22kg;
②生产甲饮料29kg,乙原料21kg;
③生产甲饮料30kg,乙原料20kg;
(2)∵生产成本要想减小,应尽可能的用完B原料,应尽可能的多生产乙饮料,少生产甲饮料,
∴生产甲原料28kg时,成本最低,
y=4×28+3×22=178元.
分析:(1)根据A、B果汁原料19千克、17.2千克,试生产两种饮料共50千克,假设生产甲种饮料x千克,那么生产甲饮料需要A,0.5xkg,乙需要A0.2(50-x)kg,0.5x+0.2(50-x)≤19,同理可得,甲,乙需要B饮料,0.3x+0.4(50-x)≤17.2,列出不等式组求出即可;
(2)根据(1)中的所求数据,可得出生产成本要想减小,应尽可能的多生产乙饮料,少生产甲饮料,结合数据可得出答案.
点评:此题主要考查了不等式组的应用,结合实际问题得出最佳方案,这是中考中的一个热点问题.
由题意得,生产甲饮料需要A,0.5xkg,乙需要A,0.2(50-x)kg,0.5x+0.2(50-x)≤19,
同理可得,甲,乙需要B饮料,0.3x+0.4(50-x)≤17.2,列出不等式组求出即可;
 ,
,解:0.5x+0.2(50-x)≤19,
解得:x≤30,
解:0.3x+0.4(50-x)≤17.2,
解得:28≤x,
∴不等式组的解集是:28≤x≤30,
有3种生产方案,分别为①生产甲饮料28kg,乙原料22kg;
②生产甲饮料29kg,乙原料21kg;
③生产甲饮料30kg,乙原料20kg;
(2)∵生产成本要想减小,应尽可能的用完B原料,应尽可能的多生产乙饮料,少生产甲饮料,
∴生产甲原料28kg时,成本最低,
y=4×28+3×22=178元.
分析:(1)根据A、B果汁原料19千克、17.2千克,试生产两种饮料共50千克,假设生产甲种饮料x千克,那么生产甲饮料需要A,0.5xkg,乙需要A0.2(50-x)kg,0.5x+0.2(50-x)≤19,同理可得,甲,乙需要B饮料,0.3x+0.4(50-x)≤17.2,列出不等式组求出即可;
(2)根据(1)中的所求数据,可得出生产成本要想减小,应尽可能的多生产乙饮料,少生产甲饮料,结合数据可得出答案.
点评:此题主要考查了不等式组的应用,结合实际问题得出最佳方案,这是中考中的一个热点问题.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
某饮料厂为了开发新产品,用A种果汁原料和B种果汁原料试制新型甲、乙两种饮料共50千克,设甲种饮料需配制x千克,两种饮料的成本总额为y元.
(1)已知甲种饮料成本每千克4元,乙种饮料成本每千克3元,请你写出y与x之间的函数关系式.
(2)若用19千克A种果汁原料和17.2千克B种果汁原料试制甲、乙两种新型饮料,下表是试验的相关数据;请你列出关于x且满足题意的不等式组,求出它的解集,并由此分析如何配制这两种饮料,可使y值最小,最小值是多少?
(1)已知甲种饮料成本每千克4元,乙种饮料成本每千克3元,请你写出y与x之间的函数关系式.
(2)若用19千克A种果汁原料和17.2千克B种果汁原料试制甲、乙两种新型饮料,下表是试验的相关数据;请你列出关于x且满足题意的不等式组,求出它的解集,并由此分析如何配制这两种饮料,可使y值最小,最小值是多少?
每千克饮料 果汁含量 果汁 |
甲 | 乙 |
| A | 0.5千克 | 0.2千克 |
| B | 0.3千克 | 0.4千克 |
某饮料厂为了开发新产品,用A、B两种果汁原料各19千克、17.2千克,试制甲、乙两种新型饮料共50千克,下表是试验的相关数据:
(1)假设甲种饮料需配制x千克,请你写出满足题意的不等式组,并求出其解集;
(2)设甲种饮料每千克成本为4元,乙种饮料每千克成本为3元,这两种饮料的成本总额为y元,请写出y与x的函数表达式,并根据(1)的运算结果,确定当甲种饮料配制多少千克时,甲、乙两种饮料的成本总额最少?
| 饮料 每千克含量 |
甲 | 乙 |
| A(单位:千克) | 0.5 | 0.2 |
| B(单位:千克) | 0.3 | 0.4 |
(2)设甲种饮料每千克成本为4元,乙种饮料每千克成本为3元,这两种饮料的成本总额为y元,请写出y与x的函数表达式,并根据(1)的运算结果,确定当甲种饮料配制多少千克时,甲、乙两种饮料的成本总额最少?

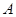 种果汁原料和
种果汁原料和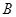 种果汁原料试制新型甲、乙两种饮料共50千克,设甲种饮料需配制
种果汁原料试制新型甲、乙两种饮料共50千克,设甲种饮料需配制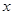 千克,两种饮料的成本总额为
千克,两种饮料的成本总额为 元.
元.