Question

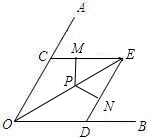如图，OE平分∠AOB，在OA、OB上取OC=OD，PM⊥CE于E，PN⊥DE于N．线段PM与PN有什么关系？证明你的结论．

Answer 1

解：PM=PN．理由如下：
证明：∵OE平分∠AOB，
∴∠COE=∠DOE．
∵OC=OD，OE=OE，
∴△COE≌△DOE（SAS）．
∴∠MEP=∠NEP，
又∵PM⊥CE，PN⊥DE，
∴PM=PN（角平分线性质）．
分析：要证PM=PN，根据角平分线的性质可知，只要证得OE平分∠CED即可得出所求结论．关键是证∠CEO和∠DEO相等，可通过证△COE和△DOE全等来实现．
点评：本题主要考查了全等三角形的判定与性质以及角平分线的性质的应用．由全等求得OE平分∠DEC是正确解答本题的关键．