Question

以O为圆心，1为半径的圆内有一定点A，过A引互相垂直的弦PQ，RS．求PQ+RS的最大值和最小值．

Answer 1

分析：设OA=a（定值），过O作OB⊥PQ，OC⊥RS，B、C为垂足，设OB=x，OC=y，0≤x≤a，（0≤y≤a），由勾股定理得出x，y，a的关系，再由垂径定理PQ和RS，最后由完全平方公式求得最大值和最小值．

解答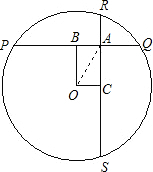：解：如图，设OA=a（定值），
过O作OB⊥PQ，OC⊥RS，B、C为垂足，
设OB=x，OC=y，0≤x≤a，（0≤y≤a），
且x²+y²=a²．
所以PQ=2PB=2

1-x2

，
RS=2（

1-x2

+

1-y2

）．
所以PQ+RS=2（

1-x2

-

1-y2

）．
∴（PQ+RS）²=4（2-a²+2

1-a2+x2y2

）
而x²y²=x²（a²-x²）=-（x²-

a2

2

）²+

a4

4

．
当x²=

a2

2

时，
（x²y²）最大值=

a4

4

．
此时PQ+RS=

4(2-a2+2-a2)

；
当x²=0或x²=a²时，（x²y²）_最小值=0，
此时（PQ+RS）_最小值=2（1+

1-a2

）．

点评：本题综合考查了垂径定理和勾股定理，以及完全平方公式的应用．解答这类题一些学生不会综合运用所学知识解答问题，不知从何处入手造成错解．