题目内容
 (1998•广东)如图,在梯形ABCD中,AD∥BC,M、N分别是BD、AC的中点,DN的延长线交BC于点E.
(1998•广东)如图,在梯形ABCD中,AD∥BC,M、N分别是BD、AC的中点,DN的延长线交BC于点E.(1)求证:△AND≌△CNE;
(2)如果BC=2AD,求证:MN=
| 1 | 2 |
分析:(1)利用AAS即可判断两三角形全等;
(2)根据(1)可得AD=EC,DN=NE,继而可判断MN是△DBE的中位线,继而可得出结论.
(2)根据(1)可得AD=EC,DN=NE,继而可判断MN是△DBE的中位线,继而可得出结论.
解答:证明:(1)在△AND和△CNE中,
∵
,
∴△AND≌△CNE;
(2)∵BC=2AD,AD=EC,
∴BE=AD,
∵△AND≌△CNE,
∴DN=NE,
∴点N是DE中点,
∴MN是△DBE的中位线,
∴MN=
BE=
AD.
∵
|
∴△AND≌△CNE;
(2)∵BC=2AD,AD=EC,
∴BE=AD,
∵△AND≌△CNE,
∴DN=NE,
∴点N是DE中点,
∴MN是△DBE的中位线,
∴MN=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了梯形、全等三角形的判定与性质及三角形的中位线定理,解答本题的关键是熟练掌握全等三角形的判定及三角形的中位线定理,难度一般.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (1998•广东)如图,三条平行线l1,l2,l3分别与另外两条直线相交于点A、C、E和点B、D、F,且AC≠CE,AC≠BD,则下列四个式子中,错误的是( )
(1998•广东)如图,三条平行线l1,l2,l3分别与另外两条直线相交于点A、C、E和点B、D、F,且AC≠CE,AC≠BD,则下列四个式子中,错误的是( )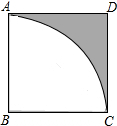 (1998•广东)如图,正方形ABCD的边长为1cm,以B为圆心,BA为半径作弧AC,则图中阴影部分面积是
(1998•广东)如图,正方形ABCD的边长为1cm,以B为圆心,BA为半径作弧AC,则图中阴影部分面积是 (1998•广东)如图是某地某一天的气温随时间变化的图象,这天最高气温比最低气温高
(1998•广东)如图是某地某一天的气温随时间变化的图象,这天最高气温比最低气温高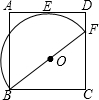 (1998•广东)如图,四边形ABCD是正方形,点F在CD上,点O是BF的中点,以BF为直径的半圆与AD相切于点E.
(1998•广东)如图,四边形ABCD是正方形,点F在CD上,点O是BF的中点,以BF为直径的半圆与AD相切于点E.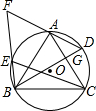 (1998•广东)如图,△ABC是⊙O的内接正三角形,D是弧AC上任一点,过C作CE∥DA交⊙O于点E,BE、DA的延长线相交于点F,连接BD交AC于点G.
(1998•广东)如图,△ABC是⊙O的内接正三角形,D是弧AC上任一点,过C作CE∥DA交⊙O于点E,BE、DA的延长线相交于点F,连接BD交AC于点G.