Question

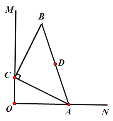
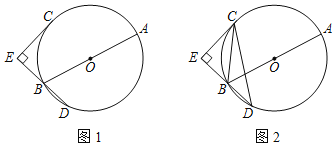
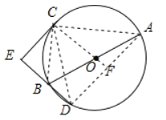
【题目】已知：AB为⊙O的直径，C、D为心⊙O上的点，C是优弧AD的中点，CE⊥DB交DB的延长线于点E．

（1）如图1，判断直线CE与⊙O的位置关系，并说明理由．

（2）如图2，若tan∠BCE＝，连BC、CD，求cos∠BCD的值．

Answer 1

【答案】（1）直线CE与⊙O相切，理由详见解析；（2）cos∠BCD＝．

【解析】

（1）如图，作辅助线；运用圆周角定理及其推论证明∠OCE＝90°，即可解决问题．

（2）首先运用切割线定理求出ED的长度；证明四边形CEDF为矩形，得到CF＝DE；证明OF为△ABD的中位线；求出AF、OF的长度；进而求出OA的长度，即可解决问题．

解：（1）直线CE与⊙O相切，理由如下：

如图，连接AC，CD，BC、AD、CO，延长CO交AD于点F；

则∠CBE＝∠CAD；而C是优弧ACD的中点，

∴，

∴∠CBA＝∠CDA＝∠CAD，

而∠CBE＝∠CAD，∠CBA＝∠OCB，

∴∠CBE＝∠OCB；而CE⊥BE，

∴∠ECB+∠CBE＝∠ECB+∠OCB＝90°，即，

∴OC⊥CE，

即CE为⊙O的切线；

（2）∵tan∠BCE＝，

设BE＝4k，CE＝5k，

∵CE为⊙O的切线，

∴CE2＝EBED，

∴ED＝k，BD＝k；

∵AB为⊙O的直径，

∴∠ADB＝90°，而∠E＝∠OCE＝90°，

∴四边形CEDF为矩形，

∴OF⊥AD，AF＝DF＝CE＝5k，

∴OF为△ABD的中位线，

∴OF＝BD＝k；由勾股定理得：OA＝＝k，

∴cos∠BAD＝＝＝，

而∠BCD＝∠BAD，

∴cos∠BCD＝．