题目内容
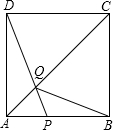 如图,在边长为4的正方形ABCD中,点P在AB上从A向B运动,连接DP交AC于点Q.
如图,在边长为4的正方形ABCD中,点P在AB上从A向B运动,连接DP交AC于点Q.(1)试证明:无论点P运动到AB上何处时,都有△ADQ≌△ABQ;
(2)当点P在AB上运动到什么位置时,△ADQ的面积是正方形ABCD面积的
| 1 | 6 |
(3)若点P从点A运动到点B,再继续在BC上运动到点C,在整个运动过程中,当点P运动到什么位置时,△ADQ恰为等腰三角形.
分析:(1)可由SAS求得△ADQ≌△ABQ;
(2)过点Q作QE⊥AD于E,QF⊥AB于F,则QE=QF,若△ADQ的面积是正方形ABCD面积的
,则有S△ADQ=
AD•QE=
S正方形ABCD,求得OE的值,再利用△DEQ∽△DAP有
=
解得AP值;
(3)点P运动时,△ADQ恰为等腰三角形的情况有三种:有QD=QA或DA=DQ或AQ=AD.由正方形的性质知,①当点P运动到与点B重合时,QD=QA,此时△ADQ是等腰三角形,②当点P与点C重合时,点Q与点C也重合,此时DA=DQ,△ADQ是等腰三角形,③当AD=AQ=4时,有CP=CQ,CP=AC-AD而由正方形的对角线的性质得到CP的值.
(2)过点Q作QE⊥AD于E,QF⊥AB于F,则QE=QF,若△ADQ的面积是正方形ABCD面积的
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 6 |
| QE |
| AP |
| DE |
| DA |
(3)点P运动时,△ADQ恰为等腰三角形的情况有三种:有QD=QA或DA=DQ或AQ=AD.由正方形的性质知,①当点P运动到与点B重合时,QD=QA,此时△ADQ是等腰三角形,②当点P与点C重合时,点Q与点C也重合,此时DA=DQ,△ADQ是等腰三角形,③当AD=AQ=4时,有CP=CQ,CP=AC-AD而由正方形的对角线的性质得到CP的值.
解答:(1)证明:在正方形ABCD中,
无论点P运动到AB上何处时,都有
AD=AB,∠DAQ=∠BAQ,AQ=AQ,
∴△ADQ≌△ABQ;
(2)解法一:△ADQ的面积恰好是正方形ABCD面积的
时,
过点Q作QE⊥AD于E,QF⊥AB于F,则QE=QF,
∵在边长为4的正方形ABCD中,
∴S正方形ABCD=16,
∴
AD×QE=
S正方形ABCD=
×16=
,
∴QE=
,
∵EQ∥AP,
∴△DEQ∽△DAP,
∴
=
,即
=
,
解得AP=2,
∴AP=2时,△ADQ的面积是正方形ABCD面积的
;
解法二:以A为原点建立如图所示的直角坐标系,过点Q作QE⊥y轴于点E,QF⊥x轴于点F.
AD×QE=
S正方形ABCD=
×16=
,
∴QE=
,
∵点Q在正方形对角线AC上,
∴Q点的坐标为(
,
),
∴过点D(0,4),Q(
,
)两点的函数关系式为:y=-2x+4,
当y=0时,x=2,
∴P点的坐标为(2,0),
∴AP=2时,即当点P运动到AB中点位置时,△ADQ的面积是正方形ABCD面积的
;
(3)解:若△ADQ是等腰三角形,则有QD=QA或DA=DQ或AQ=AD,
 ①当AD=DQ时,则∠DQA=∠DAQ=45°
①当AD=DQ时,则∠DQA=∠DAQ=45°
∴∠ADQ=90°,P为C点,
②当AQ=DQ时,则∠DAQ=∠ADQ=45°,
∴∠AQD=90°,P为B,
③AD=AQ(P在BC上),
∴CQ=AC-AQ=
BC-BC=(
-1)BC
∵AD∥BC
∴
=
,即可得
=
=1,
∴CP=CQ=(
-1)BC=4(
-1)
综上,P在B点,C点,或在CP=4(
-1)处,△ADQ是等腰三角形.
无论点P运动到AB上何处时,都有
AD=AB,∠DAQ=∠BAQ,AQ=AQ,
∴△ADQ≌△ABQ;
(2)解法一:△ADQ的面积恰好是正方形ABCD面积的
| 1 |
| 6 |
过点Q作QE⊥AD于E,QF⊥AB于F,则QE=QF,
∵在边长为4的正方形ABCD中,
∴S正方形ABCD=16,
∴

| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 6 |
| 8 |
| 3 |
∴QE=
| 4 |
| 3 |
∵EQ∥AP,
∴△DEQ∽△DAP,
∴
| QE |
| AP |
| DE |
| DA |
| ||
| AP |
4-
| ||
| 4 |
解得AP=2,
∴AP=2时,△ADQ的面积是正方形ABCD面积的
| 1 |
| 6 |
解法二:以A为原点建立如图所示的直角坐标系,过点Q作QE⊥y轴于点E,QF⊥x轴于点F.
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 6 |
| 8 |
| 3 |
∴QE=
| 4 |
| 3 |
∵点Q在正方形对角线AC上,
∴Q点的坐标为(
| 4 |
| 3 |
| 4 |
| 3 |
∴过点D(0,4),Q(
| 4 |
| 3 |
| 4 |
| 3 |
当y=0时,x=2,
∴P点的坐标为(2,0),
∴AP=2时,即当点P运动到AB中点位置时,△ADQ的面积是正方形ABCD面积的
| 1 |
| 6 |
(3)解:若△ADQ是等腰三角形,则有QD=QA或DA=DQ或AQ=AD,
 ①当AD=DQ时,则∠DQA=∠DAQ=45°
①当AD=DQ时,则∠DQA=∠DAQ=45°∴∠ADQ=90°,P为C点,
②当AQ=DQ时,则∠DAQ=∠ADQ=45°,
∴∠AQD=90°,P为B,
③AD=AQ(P在BC上),
∴CQ=AC-AQ=
| 2 |
| 2 |
∵AD∥BC
∴
| CP |
| AD |
| CQ |
| AQ |
| CP |
| CQ |
| AD |
| AQ |
∴CP=CQ=(
| 2 |
| 2 |
综上,P在B点,C点,或在CP=4(
| 2 |
点评:本题利用了正方形的性质,全等三角形和相似三角形的判定和性质,三角形的面积公式,等腰三角形的性质,等腰直角三角形的性质求解.

练习册系列答案
相关题目
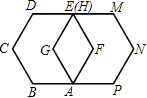 如图,如果边长为1的正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合,那么点B的对应点是点
如图,如果边长为1的正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合,那么点B的对应点是点 已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
 如图,将边长为3的正六边形A1A2A3A4A5A6,在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( )
如图,将边长为3的正六边形A1A2A3A4A5A6,在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( ) 已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心, 长为半径作
长为半径作 ,
, ,
,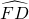 ,求阴影部分的面积.
,求阴影部分的面积. 长为半径作
长为半径作 ,
, ,
, ,求阴影部分的面积.
,求阴影部分的面积.