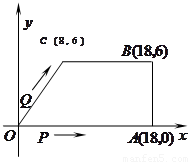题目内容
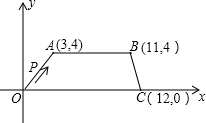
 直角坐标系中O是原点,梯形OABC各顶点的坐标如图所示,
直角坐标系中O是原点,梯形OABC各顶点的坐标如图所示,
(1)直接写出OA所在直线的解析式;
(2)求经过O、A、C三点的抛物线解析式;
(3)试在(2)中的抛物线上找一点D,使得以D、O、C为顶点的三角形与△AOC全等,请直接写出D的坐标;
(4)设P点从原点O出发,以每秒2个单位的速度沿折线O→A→B向终点B运动,求从出发起运动了t秒时P点的坐标及相应t的取值范围.
解:(1)设直线OA的解析式是y=kx,
把A(3,4)代入得:k= ,
,
∴OA所在直线的解析式是y= x.
x.
(2)∵O(0,0),C(12,0),
∴设经过O、A、C三点的抛物线解析式是y=a(x-0)(x-12),
把A(3,4)代入得:4=a(3-0)×(3-12),
解得:a=- ,
,
∴y=- (x-0)(x-12)=-
(x-0)(x-12)=- x2+
x2+ x,
x,
答:经过O、A、C三点的抛物线解析式是y=- x2+
x2+ x.
x.
(3)∵y=- x2+
x2+ x=-
x=- (x-6)2+
(x-6)2+ ,
,
∴抛物线的对称轴是直线x=6,
∵在抛物线上找一点D,使得以D、O、C为顶点的三角形与△AOC全等,A(3,4)
∴OC=OC,D于A是对应点,
∴当且仅当A、D关于直线x=6对称时,以以D、O、C为顶点的三角形才与△AOC全等,
即6-3=3,6+3=9,
∴D的坐标是(9,4).
(4) 过A作AH⊥OC于H,PN⊥OC于N,
过A作AH⊥OC于H,PN⊥OC于N,
∵A(3,4),B(11,4),
∴AB∥x轴,
∴由勾股定理得:OA=5,
分为两种情况:
①当P在OA上时,OP=2t,sin∠AOC=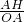 =
= =
= ,cos∠AOC=
,cos∠AOC=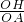 =
= =
= ,
,
解得:PN= t,ON=
t,ON= t,
t,
∴P的坐标是( t,
t, t);
t);
∵OA=5,
2t=5,
t=2.5,
∴此时t的范围是0≤t≤2.5
②当P在AB上时,P的纵坐标是4,横坐标是OH+HM=3+2(t-2.5)=2t-2,
即P的坐标是(2t-2,4),
∵11-3=8,8+5=13,13× =6.5
=6.5
∴此时t的范围是2.5≤t≤6.5.
分析:(1)直线OA的解析式是y=kx,把A(3,4)代入求出k即可;
(2)经过O、A、C三点的抛物线解析式是y=a(x-0)(x-12),把A(3,4)代入求出a即可;
(3)求出抛物线的对称轴(直线x=6),根据全等得出OC=OC,A和D是对应点,根据对称的性质得出A与D关于x=6对称时,所得的三角形和△ACO全等,根据A的坐标即可求出D的坐标;
(4)求出AO、AB,分为两种情况:①当P在OA上时,根据sin∠AOC=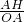 =
= =
= ,cos∠AOC=
,cos∠AOC=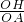 =
= =
= ,求出PN=
,求出PN= t,ON=
t,ON= t,即可得出答案;②当P在AB上时,即可得出P的纵坐标是4,横坐标是2t-5.
t,即可得出答案;②当P在AB上时,即可得出P的纵坐标是4,横坐标是2t-5.
点评:本题考查了用待定系数法求正比例函数、二次函数的解析式,全等三角形的性质和判定,勾股定理,解直角三角形等知识点的应用,主要考查学生综合运用这些性质进行计算的能力,题目综合性比较强,有一定的难度.用了分类讨论思想.
把A(3,4)代入得:k=
 ,
,∴OA所在直线的解析式是y=
 x.
x.(2)∵O(0,0),C(12,0),
∴设经过O、A、C三点的抛物线解析式是y=a(x-0)(x-12),
把A(3,4)代入得:4=a(3-0)×(3-12),
解得:a=-
 ,
,∴y=-
 (x-0)(x-12)=-
(x-0)(x-12)=- x2+
x2+ x,
x,答:经过O、A、C三点的抛物线解析式是y=-
 x2+
x2+ x.
x.(3)∵y=-
 x2+
x2+ x=-
x=- (x-6)2+
(x-6)2+ ,
,∴抛物线的对称轴是直线x=6,
∵在抛物线上找一点D,使得以D、O、C为顶点的三角形与△AOC全等,A(3,4)
∴OC=OC,D于A是对应点,
∴当且仅当A、D关于直线x=6对称时,以以D、O、C为顶点的三角形才与△AOC全等,
即6-3=3,6+3=9,
∴D的坐标是(9,4).
(4)
 过A作AH⊥OC于H,PN⊥OC于N,
过A作AH⊥OC于H,PN⊥OC于N,∵A(3,4),B(11,4),
∴AB∥x轴,
∴由勾股定理得:OA=5,
分为两种情况:
①当P在OA上时,OP=2t,sin∠AOC=
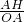 =
= =
= ,cos∠AOC=
,cos∠AOC=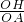 =
= =
= ,
,解得:PN=
 t,ON=
t,ON= t,
t,∴P的坐标是(
 t,
t, t);
t);∵OA=5,
2t=5,
t=2.5,
∴此时t的范围是0≤t≤2.5
②当P在AB上时,P的纵坐标是4,横坐标是OH+HM=3+2(t-2.5)=2t-2,
即P的坐标是(2t-2,4),
∵11-3=8,8+5=13,13×
 =6.5
=6.5∴此时t的范围是2.5≤t≤6.5.
分析:(1)直线OA的解析式是y=kx,把A(3,4)代入求出k即可;
(2)经过O、A、C三点的抛物线解析式是y=a(x-0)(x-12),把A(3,4)代入求出a即可;
(3)求出抛物线的对称轴(直线x=6),根据全等得出OC=OC,A和D是对应点,根据对称的性质得出A与D关于x=6对称时,所得的三角形和△ACO全等,根据A的坐标即可求出D的坐标;
(4)求出AO、AB,分为两种情况:①当P在OA上时,根据sin∠AOC=
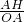 =
= =
= ,cos∠AOC=
,cos∠AOC=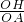 =
= =
= ,求出PN=
,求出PN= t,ON=
t,ON= t,即可得出答案;②当P在AB上时,即可得出P的纵坐标是4,横坐标是2t-5.
t,即可得出答案;②当P在AB上时,即可得出P的纵坐标是4,横坐标是2t-5.点评:本题考查了用待定系数法求正比例函数、二次函数的解析式,全等三角形的性质和判定,勾股定理,解直角三角形等知识点的应用,主要考查学生综合运用这些性质进行计算的能力,题目综合性比较强,有一定的难度.用了分类讨论思想.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 直角坐标系中O是原点,梯形OABC各顶点的坐标如图所示,
直角坐标系中O是原点,梯形OABC各顶点的坐标如图所示, 是原点,
是原点, 三点的坐标分别
三点的坐标分别 ,四边形
,四边形 是梯形,点
是梯形,点 同时从原点出发,分别作匀速运动,其中点
同时从原点出发,分别作匀速运动,其中点 沿
沿 向终点
向终点 运动,速度为每秒
运动,速度为每秒 个单位,点
个单位,点 沿
沿 向终点
向终点 运动,当这两点有一点到达自己的终点时,另一点也停止运动.
运动,当这两点有一点到达自己的终点时,另一点也停止运动.
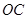 的解析式.
的解析式. 秒.如果点
秒.如果点 个单位,试写出点
个单位,试写出点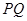 能否把梯形的面积也分成相等的两部分,如有可能,请求出
能否把梯形的面积也分成相等的两部分,如有可能,请求出 是原点,
是原点,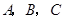 三点的坐标分别
三点的坐标分别 ,四边形
,四边形 是梯形,点
是梯形,点 同时从原点出发,分别作匀速运动,其中点
同时从原点出发,分别作匀速运动,其中点 沿
沿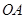 向终点
向终点 运动,速度为每秒
运动,速度为每秒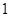 个单位,点
个单位,点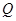 沿
沿 向终点
向终点 运动,当这两点有一点到达自己的终点时,另一点也停止运动.
运动,当这两点有一点到达自己的终点时,另一点也停止运动.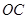 的解析式.
的解析式.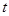 秒.如果点
秒.如果点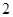 个单位,试写出点
个单位,试写出点 能否把梯形的面积也分成相等的两部分,如有可能,请求出
能否把梯形的面积也分成相等的两部分,如有可能,请求出
 是原点,
是原点,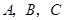 三点的坐标分别
三点的坐标分别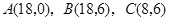 ,四边形
,四边形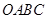 是梯形,点
是梯形,点 同时从原点出发,分别作匀速运动,其中点
同时从原点出发,分别作匀速运动,其中点 沿
沿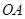 向终点
向终点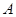 运动,速度为每秒
运动,速度为每秒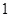 个单位,点
个单位,点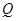 沿
沿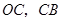 向终点
向终点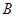 运动,当这两点有一点到达自己的终点时,另一点也停止运动.
运动,当这两点有一点到达自己的终点时,另一点也停止运动.
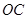 的解析式.
的解析式.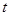 秒.如果点
秒.如果点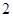 个单位,试写出点
个单位,试写出点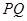 能否把梯形的面积也分成相等的两部分,如有可能,请求出
能否把梯形的面积也分成相等的两部分,如有可能,请求出 是原点,
是原点,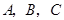 三点的坐标分别
三点的坐标分别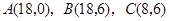 ,四边形
,四边形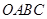 是梯形,点
是梯形,点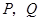 同时从原点出发,分别作匀速运动,其中点
同时从原点出发,分别作匀速运动,其中点 沿
沿 向终点
向终点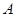 运动,速度为每秒
运动,速度为每秒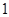 个单位,点
个单位,点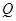 沿
沿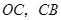 向终点
向终点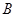 运动,当这两点有一点到达自己的终点时,另一点也停止运动.
运动,当这两点有一点到达自己的终点时,另一点也停止运动. 的解析式.
的解析式. 秒.如果点
秒.如果点 个单位,试写出点
个单位,试写出点 能否把梯形的面积也分成相等的两部分,如有可能,请求出
能否把梯形的面积也分成相等的两部分,如有可能,请求出