题目内容
如图,在直角坐标系中, 是原点,
是原点, 三点的坐标分别
三点的坐标分别 ,四边形
,四边形 是梯形,点
是梯形,点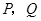 同时从原点出发,分别作匀速运动,其中点
同时从原点出发,分别作匀速运动,其中点 沿
沿 向终点
向终点 运动,速度为每秒
运动,速度为每秒 个单位,点
个单位,点 沿
沿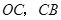 向终点
向终点 运动,当这两点有一点到达自己的终点时,另一点也停止运动.
运动,当这两点有一点到达自己的终点时,另一点也停止运动.
(1)求直线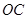 的解析式.
的解析式.
(2)设从出发起,运动了 秒.如果点
秒.如果点 的速度为每秒
的速度为每秒 个单位,试写出点
个单位,试写出点 的坐标,并写出此时
的坐标,并写出此时 的取值范围.
的取值范围.
(3)设从出发起,运动了 秒.当
秒.当 ,
, 两点运动的路程之和恰好等于梯形
两点运动的路程之和恰好等于梯形 的周长的一半,这时,直线
的周长的一半,这时,直线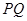 能否把梯形的面积也分成相等的两部分,如有可能,请求出
能否把梯形的面积也分成相等的两部分,如有可能,请求出 的值;如不可能,请说明理由.
的值;如不可能,请说明理由.
(1) 两点的坐标分别为
两点的坐标分别为 ,
,
设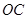 的解析式为
的解析式为 ,
,
将两点坐标代入得: ,
, .
. .
.
(2)当 在
在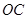 上运动时,
上运动时,
可设 ,依题意有:
,依题意有: ,
, .
.
 .
.
当 在
在 上运动时,
上运动时, 点所走过的路程为
点所走过的路程为 .
. .
. 点的横坐标为
点的横坐标为 .
. .
.
(3) 梯形
梯形 的周长为
的周长为 ,
,
当 点在
点在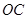 上运动时,
上运动时, 运动的路程为
运动的路程为 ,则
,则 运动的路程为
运动的路程为 .
. 中,
中, 边上的高为:
边上的高为: .
. ,
, .
.
依题意有: .
.
整理得: .
. ,
, 这样的
这样的 不存在.
不存在.
当 在
在 上运动时,
上运动时, 走过的路程为
走过的路程为 ,
, 的长为:
的长为: .
. .
. 这样的
这样的 值也不存在.
值也不存在.
综上所述,
不存在这样的 值,使得
值,使得 ,
, 两点同时平分梯形的周长和面积.
两点同时平分梯形的周长和面积.
解析

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目

 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: