题目内容
【题目】完成下面的证明过程：
已知：如图，
，
，
．
求证：
．
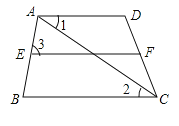
证明：∵，（已知）
∴
．
∴
，（ ）
又∵，（已知）
∴______
，（内错角相等，两直线平行）
∴
_______，（ ）
∴．（ ）
【答案】同旁内角互补，两直线平行；AD；BC；如果两条直线平行于第三条直线，那么它们互相平行；两直线平行，同位角相等．
【解析】
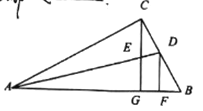
求出∠D＋∠EFD＝180
，根据平行线的判定得出AD∥EF和 AD∥BC，即可得出EF∥BC，根据平行线的性质得出即可．
证明：∵∠D＝123，∠EFD＝57（已知），
∴∠D＋∠EFD＝180，
∴AD∥EF（同旁内角互补，两直线平行），
又∵∠1＝∠2（已知）
∴AD∥BC（内错角相等，两直线平行）
∴EF∥BC（平行于同一条直线的两直线平行），
∴∠3＝∠B（两直线平行，同位角相等），
故答案为：同旁内角互补，两直线平行；AD；BC；如果两条直线平行于第三条直线，那么它们互相平行；两直线平行，同位角相等．
练习册系列答案
中考解读考点精练系列答案
各地期末复习特训卷系列答案
相关题目
