题目内容
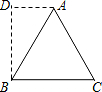
如图，在等边三角形ABC外作正方形ACDE，AD与BE交于点F，则∠FCD=
- A.60°
- B.45°
- C.75°
- D.54°
C
分析：根据已知证明△AFE≌△AFC，从而得到∠ACF的度数，从而不难求得∠FCD的度数．
解答：∵AB=AE=AC=CD
∴∠ABE=∠AEB=15°
∵∠CAF=∠EAF=45°，AF=AF，AC=AE
∴△AFE≌△AFC
∴∠ACF=∠AEC=15°
∴∠FCD=90°-15°=75°
故选C．
点评：主要考查了正方形对角线相互垂直平分相等和等边三角形的特殊性质的综合运用．
分析：根据已知证明△AFE≌△AFC，从而得到∠ACF的度数，从而不难求得∠FCD的度数．
解答：∵AB=AE=AC=CD
∴∠ABE=∠AEB=15°
∵∠CAF=∠EAF=45°，AF=AF，AC=AE
∴△AFE≌△AFC
∴∠ACF=∠AEC=15°
∴∠FCD=90°-15°=75°
故选C．
点评：主要考查了正方形对角线相互垂直平分相等和等边三角形的特殊性质的综合运用．
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
相关题目
如图，在等边三角形ABC的边BC、AC上分别取点D、E，使BD=CE，AD与BE相交于点P．则∠APE的度数为
9、如图，在等边三角形ABC中，三条中线AE，BD，CF相交于点O，则等边三角形ABC中，从△BOF到△COD需要经过的变换是（ ）
如图，在等边三角形ABC中，BD⊥BC，过A作AD⊥BD于D，已知△ABC周长为M，则AD=（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
如图，在等边三角形ABC的AC边上取中点D，BC的延长线上取一点E，使CE=CD，求证：△BDE为等腰三角形．
如图，在等边三角形△ABC中，AQ=PQ，PR⊥AB于点R，PS⊥AC于点S，且PR=PS，下面给出的四个结论：①点P在∠A的平分线上，②AS=AR，③QP∥AR，④△BRP≌△QSP，则其中正确的是（ ）