题目内容
已知点E是平行四边形ABCD的边AB延长线上一点，且BE=| 2 | 3 |
（1）求EF：FD与CG：AG；
（2）若FG=GD-3，试求EF的长．
分析：（1）通过△BEF∽△AED的对应边成比例得到：
=
，则
=
=
，即EF：FD=2：3；同理由△FCG∽△DAG的对应边成比例求得CG：AG=3：5；
（2）由△FCG∽△DAG，得到：
=
=
，易求GD=7.5，故FG=4.5，则FD=12．所以由
=
求得EF=8．
| EF |
| ED |
| EB |
| EA |
| EF |
| FD |
| BE |
| BA |
| 2 |
| 3 |
（2）由△FCG∽△DAG，得到：
| CG |
| AG |
| FG |
| GD |
| 3 |
| 5 |
| EF |
| FD |
| 2 |
| 3 |
解答：解：（1）如图，
∵四边形ABCD是平行四边形，
∴BC∥AD，BC=AD，
∴△BEF∽△AED，△FCG∽△DAG，
∴
=
=
=
，
=
，
∴
=
=
，即EF：FD=2：3；
=
=
=
=
=
，即CG：AG=3：5；
（2）由△FCG∽△DAG，得到：
=
=
，
∵FG=GD-3，
∴
=
，则GD=7.5，
∴FG=4.5，
∴FD=12．
∵
=
，
∴EF=8．
∵四边形ABCD是平行四边形，
∴BC∥AD，BC=AD，
∴△BEF∽△AED，△FCG∽△DAG，
∴
| EF |
| ED |
| EB |
| EA |
| BF |
| AD |
| 2 |
| 5 |
| CG |
| AG |
| FC |
| AD |
∴
| EF |
| FD |
| BE |
| BA |
| 2 |
| 3 |
| CG |
| AG |
| FC |
| AD |
| BC-BF |
| AD |
AD-
| ||
| AD |
AD-
| ||
| AD |
| 3 |
| 5 |
（2）由△FCG∽△DAG，得到：
| CG |
| AG |
| FG |
| GD |
| 3 |
| 5 |
∵FG=GD-3，
∴
| GD-3 |
| GD |
| 3 |
| 5 |
∴FG=4.5，
∴FD=12．
∵
| EF |
| FD |
| 2 |
| 3 |
∴EF=8．
点评：本题考查了平行四边形的性质，相似三角形的判定与性质．相似三角形相似多边形的特殊情形，它沿袭相似多边形的定义，从对应边的比相等和对应角相等两方面下定义；反过来，两个三角形相似也有对应角相等，对应边的比相等．
练习册系列答案
相关题目
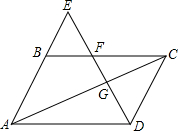已知点E是平行四边形ABCD的边AB延长线上一点，且BE=
AB，DE分别交BC、AC于点F、G．