题目内容
(1)已知a=-
,b=2,c=-2
,求代数式ab-a2c的值;
(2)若|a-3|+(b+2)2=0,求ba-3b的值.
| 1 |
| 2 |
| 1 |
| 2 |
(2)若|a-3|+(b+2)2=0,求ba-3b的值.
分析:(1)将a,b及c的值代入所求式子中计算,即可求出值;
(2)由两个非负数之和为0,得到两非负数分别为0,求出a与b的值,将a与b的值代入所求式子中计算,即可求出值.
(2)由两个非负数之和为0,得到两非负数分别为0,求出a与b的值,将a与b的值代入所求式子中计算,即可求出值.
解答:解:(1)当a=-
,b=2,c=-2
时,
ab-a2c=-
×2-(-
)2×(-2
)=-1-
×(-
)=-1+
=-
;
(2)∵|a-3|+(b+2)2=0,
∴a-3=0且b+2=0,即a=3,b=-2,
则ba-3b=(-2)3-3×(-2)=-8+6=-2.
| 1 |
| 2 |
| 1 |
| 2 |
ab-a2c=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 5 |
| 2 |
| 5 |
| 8 |
| 3 |
| 8 |
(2)∵|a-3|+(b+2)2=0,
∴a-3=0且b+2=0,即a=3,b=-2,
则ba-3b=(-2)3-3×(-2)=-8+6=-2.
点评:此题考查了代数式求值,以及非负数的性质,熟练掌握两个非负数之和为0,得到两非负数分别为0是解本题第二小题的关键.

练习册系列答案
相关题目
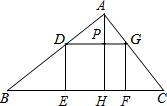 如图,矩形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,AH⊥BC,垂足为H.已知BC=12,AH=8.当矩形DEFG面积最大时,求矩形的长和宽.
如图,矩形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,AH⊥BC,垂足为H.已知BC=12,AH=8.当矩形DEFG面积最大时,求矩形的长和宽.