题目内容
如图,直线 (
( >0)与双曲线
>0)与双曲线 在第一象限内的交点面积为R,与
在第一象限内的交点面积为R,与 轴的交点为P,与
轴的交点为P,与 轴的交点为Q;作RM⊥
轴的交点为Q;作RM⊥ 轴于点M,若△OPQ与△PRM的面积是4:1,则
轴于点M,若△OPQ与△PRM的面积是4:1,则

【答案】

【解析】∵Rt△OQP∽Rt△MRP,
而△OPQ与△PRM的面积比是4:1,
∴OQ:RM=2:1,
∵Q为 =k
=k -2与
-2与 轴交点,
轴交点,
∴OQ=2,
∴RM=1,即R的纵坐标为1,
把 =1代入直线
=1代入直线 =
=

 -2,得
-2,得 =
= ,
,
所以R的坐标为( ,1),把它代入
,1),把它代入 ,得
,得 ×1=
×1= (
( >0),解得
>0),解得 =±
=± .
.
∵图象在第一三象限,
∴ =
= ,
,

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 如图,直线y=-x+b与双曲线y=-
如图,直线y=-x+b与双曲线y=- 如图,直线
如图,直线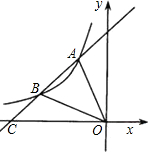 如图,直线y=kx+b与反比例函数y=
如图,直线y=kx+b与反比例函数y= (2013•大兴区二模)已知:如图,直线y=-
(2013•大兴区二模)已知:如图,直线y=- 如图,直线y=-2x+4与x轴、y轴分别相交于A、B两点,P是直线AB上的一个动点,点C的坐标为(-4,0),PC交y轴于点D,O是原点.
如图,直线y=-2x+4与x轴、y轴分别相交于A、B两点,P是直线AB上的一个动点,点C的坐标为(-4,0),PC交y轴于点D,O是原点.