题目内容
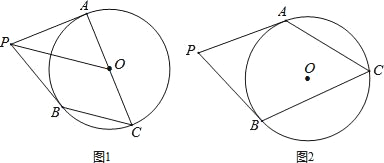
【题目】已知P为⊙O外一点,PA、PB分别切⊙O于A、B两点,点C为⊙O上一点.
(1)如图1,若AC为直径,求证:OP∥BC;
(2)如图2,若sin∠P=![]() ,求tanC的值.
,求tanC的值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)连接AB交PO于M,根据切线性质得出PA=PB,OP平分∠APB,推出∠AMO=90°,根据平行线的判定推出即可;
(2)求出∠E=∠C,求出∠E=∠PBA,解直角三角形求出即可.
试题解析:(1)证明:连接AB交PO于M,
∵PA、PB分别切⊙O于A、B两点,
∴PA=PB,OP平分∠APB,
∴AB⊥OP,
∴∠AMO=90°,
∵AC为直径,
∴∠ABC=90°,
∴∠AMO=∠ABC,
∴OP∥BC;
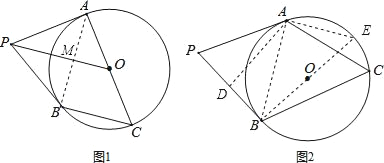
(2)连接AB,过A作AD⊥PB于D,作直径BE,连接AE,
∵PB为⊙O的切线,
∴BE⊥PB,
∴∠PBA+∠ABE=90°,
∵BE为直径,
∴∠BAE=90°,
∴∠E+∠ABE=90°,
∴∠E=∠ABP,
∵∠E=∠C,
∴∠C=∠ABP,
∵sin∠P=![]() ,
,
∴设AD=12x,则PA=13x,PD=5x,
∴BD=8x,
∴tan∠ABD=![]() ,
,
∴tan∠C=![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】探究逼近![]() 的有理近似值.
的有理近似值.
方法介绍:
经过![]() 步操作(
步操作(![]() 为正整数)不断寻找有理数
为正整数)不断寻找有理数![]() ,
,![]() ,使得
,使得![]() ,并且让
,并且让![]() 的值越来越小,同时利用数轴工具将任务几何化,直观理解通过等分线段的方法不断缩小
的值越来越小,同时利用数轴工具将任务几何化,直观理解通过等分线段的方法不断缩小![]() 对应的点
对应的点![]() 所在线段的长度(二分法)
所在线段的长度(二分法)
思路
在数轴上记![]() ,
,![]() 对应的点分别为
对应的点分别为![]() ,
,![]() 和
和![]() 的平均数
的平均数![]() 对应线段
对应线段![]() 的中点(记为
的中点(记为![]() ).通过判断
).通过判断![]() 还是
还是![]() ,得到点
,得到点![]() 是在二等分后的“左线段
是在二等分后的“左线段![]() ”上还是“右线段
”上还是“右线段![]() ”上,重复上述步骤,不断得到
”上,重复上述步骤,不断得到![]() ,从而得到
,从而得到![]() 更精确的近似值.
更精确的近似值.
具体操作步骤及填写“阅读活动任务单”:
(1)当![]() 时,
时,
①寻找左右界值:先寻找两个连续正整数![]() ,使得
,使得![]() .
.
因为![]() ,所以
,所以![]() ,那么
,那么![]() ,
,![]() ,线段
,线段![]() 的中点
的中点![]() 对应的数
对应的数![]() .
.
②二分定位:判断点![]() 在“左线段
在“左线段![]() ”上还是在“右线段
”上还是在“右线段![]() ”上.
”上.
比较7与![]() 的大小,从而确定
的大小,从而确定![]() 与
与![]() 的大小;
的大小;
因为![]() >
> ![]() (填 “>”或“<”),得到点
(填 “>”或“<”),得到点![]() 在线段
在线段 ![]() 上(填“
上(填“![]() ”或“
”或“![]() ”).
”).
(2)当![]() 时,在(1)中所得
时,在(1)中所得![]() 的基础上,仿照以上步骤,继续进行下去,得到表中
的基础上,仿照以上步骤,继续进行下去,得到表中![]() 时的相应内容.
时的相应内容.
请继续仿照以上步骤操作下去,补全“阅读活动任务单”:
|
|
|
|
| 点 | 得出更精确的 |
1 | 2 | 3 | 2.5 |
| 点 |
|
2 | 2.5 | 3 | 2.75 |
| 点 |
|
3 | 2.5 | 2.75 | 2.625 |
| ||
4 |