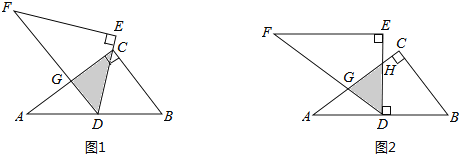题目内容
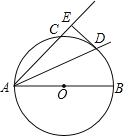
【题目】如图,AB为⊙O的直径,AC为⊙O的弦,AD平分∠BAC,交⊙O于点D,DE⊥AC,交AC的延长线于点E.
(1)求证:直线DE是⊙O的切线;
(2)若AE=8,⊙O的半径为5,求DE的长.
【答案】(1)见解析;(2)4
【解析】
(1)连接OD,由角平分线和等腰三角形的性质得出∠ODA=EAD,证出EA∥OD,再由已知条件得出DE⊥OD,即可得出结论.
(2)作DF⊥AB,垂足为F,由AAS证明△EAD≌△FAD,得出AF=AE=8,DF=DE,求出OF=3,由勾股定理得出DF,即可得出结果.
(1)证明:连接OD,如图1所示:
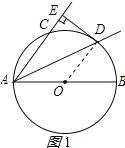
∵AD平分∠BAC,
∴∠EAD=∠OAD,
∵OA=OD,
∴∠ODA=∠OAD,
∴∠ODA=∠EAD,
∴EA∥OD,
∵DE⊥EA,
∴DE⊥OD,
∵点D在⊙O上,
∴直线DE与⊙O相切.
(2)作DF⊥AB,垂足为F,如图2所示:
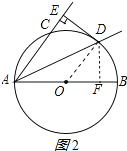
作![]() ,垂足为F,如图2所示:
,垂足为F,如图2所示:
![]() ,
,
在![]() 和
和![]() 中,
中,
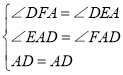 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() .
.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
【题目】已知二次函数![]() 中的
中的![]() ,
,![]() 满足下表
满足下表
| … |
| 0 | 1 | 2 | 3 | … |
| … | 0 |
|
|
|
| … |
(l)![]() ________,
________,![]() ________;
________;
(2)函数图象对称轴是____________;
(3)如果点![]() ,
,![]() 是图象上点,则
是图象上点,则![]() ________;
________;
(4)函数图象与![]() 轴交于点
轴交于点![]() 、点
、点![]() ,
,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,则点
,则点![]() 坐标为________.
坐标为________.