Question

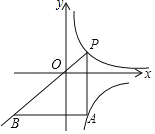
【题目】已知点在抛物线的图象上，且则线段长的最大值与最小值的差为（ ）

A.B.C.D.

Answer 1

【答案】C

【解析】

由点A、B在抛物线上，可用t表示y1、y2，根据两点间距离公式用t表示AB2，发现AB2与t是二次函数的关系，由抛物线性质和自变量t的取值范围可知：t在对称轴上时取得最小值；观察t本身的取值范围，看t＝2和t＝2哪个离对称轴更远，即对应的函数值最大．

∵点A（t，y1），B（t＋2，y2）在抛物线的图象上

∴y1＝t2，y2＝（t＋2）2＝t2＋2t＋2

∴AB2＝（t＋2t）2＋（y2y1）2＝22＋（t2＋2t＋2t2）2＝4＋（2t＋2）2＝4（t＋1）2＋4

∴AB2与t是二次函数的关系，由抛物线性质可知：

当t＝1时，AB2取得最小值，AB2＝4，AB＝2

当t＝2时，AB2取得最大值，AB2＝4×（2＋1）2＋4＝40，AB＝2

∴最大值与最小值的差为，

故选：C．