题目内容
 如图所示,点A、B分别为两个村庄,AB、BC、CD为公路,BD为农田,AD为河宽,且CD与AD互相垂直.经测量得AB=4
如图所示,点A、B分别为两个村庄,AB、BC、CD为公路,BD为农田,AD为河宽,且CD与AD互相垂直.经测量得AB=4 千米,BC=10千米,CE=6千米,∠BDC=45°,∠ABD=15°.
千米,BC=10千米,CE=6千米,∠BDC=45°,∠ABD=15°.
(1)求出河宽AD(结果保留根号);
(2)求出公路CD的长.
 解:作BF⊥AF,BG⊥CD,
解:作BF⊥AF,BG⊥CD,(1)则∠BAF=60°,∴BF=ABsin60°=6,AF=ABcos60°=2
 ,
,∠BDA=90°-∠BDC=45°,
∴DF=BFtan45°=6,
∴AD=6-2
 ;
;(2)∵BG∥DF,BF∥GD,AD⊥CD,
四边形BFDG为矩形,
又∠BDC=45°,
∴四边形BFDG为正方形,
∴BG=DF=6,BF=DG=6,
在Rt△BCG中,BC=10,BG=6,
CG=
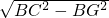 =8,
=8,∴CD长度为6+8=14.
分析:(1)分别作BF⊥AF,BG⊥CD,解直角△ABF可求得AF、BF,解直角△BDF可求得DF的长,根据AF、DF可以求得AD的长;
(2)易证四边形BFDG为矩形,则DG=BF,在直角△BCG中,根据勾股定理即可求得CG的长,根据CG、DG即可求CD的长.
点评:本题考查了勾股定理在直角三角形中的运用,特殊角的三角函数值的计算,三角函数在直角三角形中的运用.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 3、如图所示,点M,N分别是正八边形相邻两边AB,BC上的点,且AM=BN,则∠MON=
3、如图所示,点M,N分别是正八边形相邻两边AB,BC上的点,且AM=BN,则∠MON= 如图所示,点D、E分别是AB、AC的中点,点F、G分别为BD、CE的中点,若FG=6,则DE+BC=
如图所示,点D、E分别是AB、AC的中点,点F、G分别为BD、CE的中点,若FG=6,则DE+BC=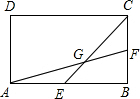 如图所示,点E,F分别是矩形ABCD的边AB,BC的中点,连接AF,EC交于点G,则
如图所示,点E,F分别是矩形ABCD的边AB,BC的中点,连接AF,EC交于点G,则