题目内容
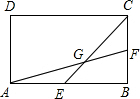 如图所示,点E,F分别是矩形ABCD的边AB,BC的中点,连接AF,EC交于点G,则
如图所示,点E,F分别是矩形ABCD的边AB,BC的中点,连接AF,EC交于点G,则| S四边形BFGE |
| S四边形AGCD |
| 1 |
| 4 |
| 1 |
| 4 |
分析:首先将四边形BFGE分成两个三角形,由等高的三角形的面积的比等于对应底的比,利用方程思想求解即可.
解答: 解:如图:
解:如图:
连接BG,设S△AEG=a,S△CFG=b,
∵点E,F分别是矩形ABCD的边AB,BC的中点,
∴S△BEG=a,
∴S△BGF=S△FGC=b,
∴S△ABF=S△BCE=
S矩形ABCD,S△ABF=2a+b,S△BCE=2b+a,
∴a=b,S矩形ABCD=12a,
∴
=
=
.
故答案为:
.
 解:如图:
解:如图:连接BG,设S△AEG=a,S△CFG=b,
∵点E,F分别是矩形ABCD的边AB,BC的中点,
∴S△BEG=a,
∴S△BGF=S△FGC=b,
∴S△ABF=S△BCE=
| 1 |
| 4 |
∴a=b,S矩形ABCD=12a,
∴
| S四边形BFGE |
| S四边形AGCD |
| 2a |
| 8a |
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
点评:此题考查了不规则图形的面积的求解方法:注意将原图形分割求解.解此题的关键是注意等高的三角形的面积的比等于对应底的比.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
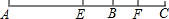
 3、如图所示,点M,N分别是正八边形相邻两边AB,BC上的点,且AM=BN,则∠MON=
3、如图所示,点M,N分别是正八边形相邻两边AB,BC上的点,且AM=BN,则∠MON= 如图所示,点D、E分别是AB、AC的中点,点F、G分别为BD、CE的中点,若FG=6,则DE+BC=
如图所示,点D、E分别是AB、AC的中点,点F、G分别为BD、CE的中点,若FG=6,则DE+BC=