题目内容
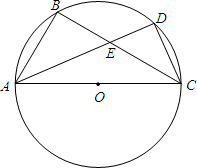（2013•峨眉山市二模）如图，AC是⊙O直径，△ABC内接于⊙O，E是BC边上一个动点（与B、C不重合），连结AE，并延长交⊙O于点D，连结CD．已知⊙O的半径为1，∠BAC=60°．（1）当E为BC的中点时，求
| AE |
| CD |
（2）设CE为x，求
| AE |
| CD |
（3）能否找到一个点E，使得
| AE |
| CD |
| 3 |
分析：（1）求出BC、BE、CE的长，根据勾股定理求出AE，证△AEB∽△CED，得出比例式，求出DC，代入求出即可；
（2）求出BC、BE、CE的长，根据勾股定理求出AE，证△AEB∽△CED，得出比例式，求出DC，代入求出即可；
（3）根据（2）的结果得出方程，求出发出的解即可．
（2）求出BC、BE、CE的长，根据勾股定理求出AE，证△AEB∽△CED，得出比例式，求出DC，代入求出即可；
（3）根据（2）的结果得出方程，求出发出的解即可．
解答：解：（1）∵AC是⊙O直径，
∴∠ABE=∠ADC=90°，
∵∠BAC=60°，AC=1+1=2，
∴∠BCA=30°，
∴AB=1，由勾股定理得：BC=
，
∵E为BC的中点，
∴CE=BE=
，
在Rt△ABE中，由勾股定理得：AE=
=
，
∵∠ABE=∠ADC=90°，∠AEB=∠DEC，
∴△AEB∽△CED，
∴
=
，
∴CD=
=
，
∴
=
=
．
（2）∵CE=x，
∴BE=
-x，
在Rt△ABE中，由勾股定理得：AE=
，
∵∠ABE=∠ADC=90°，∠AEB=∠DEC，
∴△AEB∽△CED，
∴
=
，
∴CD=
，
∴
=
=
．
（3）假设存在E点，使得
=8-2
，
则
=8-2
，
解得：x=4+2
（大于直径AC的长2，舍去），x=4-2
，
即存在E点，使得
=8-2
，此时CE=4-2
．
∴∠ABE=∠ADC=90°，
∵∠BAC=60°，AC=1+1=2，
∴∠BCA=30°，
∴AB=1，由勾股定理得：BC=
| 3 |
∵E为BC的中点，
∴CE=BE=
| ||
| 2 |
在Rt△ABE中，由勾股定理得：AE=
12+(
|
| ||
| 2 |
∵∠ABE=∠ADC=90°，∠AEB=∠DEC，
∴△AEB∽△CED，
∴
| AB |
| DC |
| AE |
| CE |
∴CD=
1×
| ||||
|
| ||
| 7 |
∴
| AE |
| CD |
| ||||
|
7
| ||
| 6 |
（2）∵CE=x，
∴BE=
| 3 |
在Rt△ABE中，由勾股定理得：AE=
12+(
|
∵∠ABE=∠ADC=90°，∠AEB=∠DEC，
∴△AEB∽△CED，
∴
| AB |
| DC |
| AE |
| CE |
∴CD=
| x | ||||
|
∴
| AE |
| CD |
| ||||||
|
4-2
| ||
| x |
（3）假设存在E点，使得
| AE |
| CD |
| 3 |
则
4-2
| ||
| x |
| 3 |
解得：x=4+2
| 3 |
| 3 |
即存在E点，使得
| AE |
| CD |
| 3 |
| 3 |
点评：本题考查了圆周角定理，勾股定理，含30度角的直角三角形性质，相似三角形的性质和判定等知识点的应用，主要考查学生的推理和计算能力，题目比较典型，是一道比较好的题目．
练习册系列答案
阅读快车系列答案
相关题目
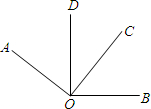（2013•峨眉山市二模）如图所示，已知∠BOC=55°，∠AOC=∠BOD=90°，则∠AOD为（ ）