Question

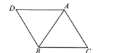
【题目】如图，已知等边，，将绕点A顺时针旋转，得到，点E是某边的一点，当为直角三角形时，连接，作于F，那么的长度是_________________

Answer 1

【答案】或

【解析】

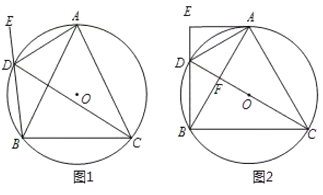
分两种情况：①点在上，如图1，利用面积面积求解；②当点在上，如图2，利用直角面积的不同求法求解长．

解：分两种情况：

①当点在上，如图1，

∵为直角三角形,

∴AE⊥BC，

∵为等边三角形，

∴是中点，

，．

∵∠DAB=∠ABC=60°

∴，

∴，

∴，

∵面积面积．

,

即，,

．

②当点在上，如图2，

作于

∵为直角三角形,

∴BE⊥AC，

∵为等边三角形，

∴是中点， ∠EBC=30°,

，

∵△ABC, △ADB都是等边三角形，

∴∠ABD=60°,∠EAG=60°,

∴∠AEG=90°-∠EAG=30°，∠DBE=∠DBA+∠ABE=90°

∴AG=,，

∴

∴

∵面积为，

，可得．

故答案为或．