Question

如图，B、D、C三点在同一直线上，△ABD和△CDE都是等腰直角三角形，∠BAD=∠DCE=90°，F是BE中点，判断FA与FC的关系并证明你的结论．

Answer 1

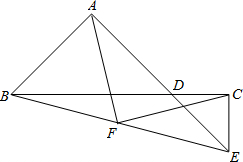
FA=FC，理由如下：
∵∠BAD=90°，点F是BE的中点，
∴在Rt△ABE中，AF是斜边BE的中线，
∴FA=BF=

1

2

BE（直角三角形斜边上的中线等于斜边的一半）．
同理，在Rt△BCE中，FC=EF=

1

2

BE，
∴FA=FC（等量代换）．