题目内容
【题目】如图,已知A、B两点的坐标分别为(-4,0)、(0,2),⊙C的圆心坐标为(0,-2),半径为2.若D是⊙C上的一个动点,射线AD与 ![]() 轴交于点E,则△ABE面积的最大值是 .
轴交于点E,则△ABE面积的最大值是 . 
【答案】![]()
【解析】当射线AD与⊙C相切时,△ABE面积的最大.
如图,连接AC.
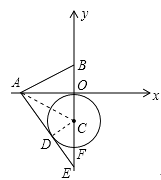
∵A点的坐标为(-4,0),⊙C的圆心坐标为(0,-2),半径为2.
∴AO=4,OC=2,即OC为⊙C的半径,则AO与⊙C相切.
∵AO、AD是⊙C的两条切线,
∴AD=AO=4.
连接CD,设EF=x,
∴DE2=EFOE,
∵CF=2,
∴DE= ![]() .
.
易证△CDE∽△AOE,则 ![]() ,即
,即 ![]() ,
,
解得x= ![]() 或x=0(不合题意,舍去),
或x=0(不合题意,舍去),
∴BE=BO+OF+EF=2+4+ ![]() =
= ![]()
故△ABE面积的最大值为: ![]() =
= ![]() .
.
【考点精析】本题主要考查了相似三角形的判定与性质的相关知识点,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案【题目】某电器商城销售![]() 、
、![]() 两种型号的电风扇,进价分别为
两种型号的电风扇,进价分别为![]() 元、
元、![]() 元,下表是近两周的销售情况:
元,下表是近两周的销售情况:
销售时段 | 销售型号 | 销售收入 | |
|
| ||
第一周 |
|
|
|
第二周 |
|
|
|
(1)求![]() 、
、![]() 两种型号的电风扇的销售单价;
两种型号的电风扇的销售单价;
(2)若商城准备用不多于![]() 元的金额再采购这两种型号的电风扇共
元的金额再采购这两种型号的电风扇共![]() 台,求
台,求![]() 种型号的电风扇最多能采购多少台?
种型号的电风扇最多能采购多少台?
(3)在(2)的条件下商城销售完这![]() 台电风能否实现利润超过
台电风能否实现利润超过![]() 元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
【题目】某学校兴趣小组,对函数y=|x﹣1|+1的图像和性质进行了研究,探究过程如下:
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值如表:
的几组对应值如表:
X | …… |
|
|
| 0 | 1 | 2 | 3 | 4 | 5 | …… |
y | …… | 5 | 4 | m | 2 | 1 | 2 | 3 | 4 | 5 | …… |
其中![]()
(2)在平面直角坐标系中,画出上表中对应值为点的坐标,根据画出的点,画出该函数的图象;

(3)根据画出的函数图像特征,仿照示例,完成下表中函数的变化规律:
序号 | 函数图像特征 | 函数变化规律 |
示例1 | 在直线 | 当 |
① | 在直线 |
|
示例2 | 函数图像经过点(-3,5) | 当 |
② | 函数图像的最低点是 | 当 |
(4)当![]() 时,
时,![]() 的取值范围是_____________
的取值范围是_____________





