题目内容
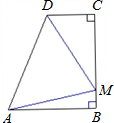 如图,ABCD为直角梯形(∠B=∠C=90°),且AB=BC,若在边BC上存在一点M,使得△AMD为等边三角形,则
如图,ABCD为直角梯形(∠B=∠C=90°),且AB=BC,若在边BC上存在一点M,使得△AMD为等边三角形,则 的值为________.
的值为________.
 -1
-1分析:首先过点D作DH⊥AB于H,易得四边形DHBC是矩形,即可得DH=BC=AB,BH=DC,然后设CD=x,AB=BC=DH=y,CM=z,在Rt△CDM,Rt△ABM,Rt△ADH中,由勾股定理可得方程组:x2+z2=y2+(y-z)2,y2+(y-z)2=y2+(y-x)2,即可得x2=2y2-2yx,然后方程两边同除以y2,即可得方程(
 )2+
)2+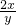 -2=0,解此方程即可求得
-2=0,解此方程即可求得 的值.
的值.解答:
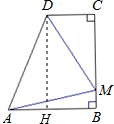 解:过点D作DH⊥AB于H,
解:过点D作DH⊥AB于H,则∠DHA=90°,
∵∠B=∠C=90°
∴四边形DHBC是矩形,
∴DH=BC,BH=DC,
∵BC=AB,
∴DH=BC=AB,
设CD=x,AB=BC=DH=y,CM=z,
在Rt△CDM,Rt△ABM,Rt△ADH中,
DM2=CD2+CM2,①
AM2=AB2+BM2,②
AD2=AH2+DH2,③
当DM=AM=AD时,△AMD为等边三角形,
则CD2+CM2=AB2+BM2,
AB2+BM2=AH2+DH2,
即x2+z2=y2+(y-z)2④,
y2+(y-z)2=y2+(y-x)2⑤,
化简④得:x2=2y2-2yz,
化简⑤得:x=z,
∴x2=2y2-2yx,
即(
 )2+
)2+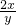 -2=0,
-2=0,解得:
 =
= -1,
-1, =-
=- -1(舍去).
-1(舍去).故
 的值为
的值为 -1.
-1.点评:此题考查了直角梯形的性质、勾股定理、等边三角形的性质以及方程组的应用.此题难度较大,解题的关键是作出辅助线,利用勾股定理得方程组,化简求得(
 )2+
)2+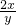 -2=0是解此题的关键.
-2=0是解此题的关键. 
练习册系列答案
相关题目
 如图,ABCD是直角梯形,以斜腰AB为直径作圆,交CD于点E,F,交BC于点G.
如图,ABCD是直角梯形,以斜腰AB为直径作圆,交CD于点E,F,交BC于点G.
 如图,ABCD是直角梯形,AB=18cm,CD=15cm,AD=6cm,点P从B点开始,沿BA边向点A以1cm/s的速度移动,点Q从D点开始,沿DC边向点C以2cm/s的速度移动,如果P、Q分别从B、D同时出发,P、Q有一点到达终点时运动停止,设移动时间为t.
如图,ABCD是直角梯形,AB=18cm,CD=15cm,AD=6cm,点P从B点开始,沿BA边向点A以1cm/s的速度移动,点Q从D点开始,沿DC边向点C以2cm/s的速度移动,如果P、Q分别从B、D同时出发,P、Q有一点到达终点时运动停止,设移动时间为t. 如图,ABCD是直角梯形,以斜腰AB为直径作圆,交CD于点E,F,交BC于点G.
如图,ABCD是直角梯形,以斜腰AB为直径作圆,交CD于点E,F,交BC于点G. .
. .
.