题目内容
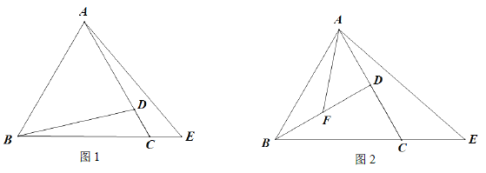
【题目】在等边![]() 中,点D在线段AC上,E为BC延长线上一点,且CD = CE,连接BD,连接AE.
中,点D在线段AC上,E为BC延长线上一点,且CD = CE,连接BD,连接AE.
(1)如图1,若![]() ,求线段AD的长;
,求线段AD的长;
(2)如图2,若F是线段BD的中点,连接AF,若![]() ,求证:
,求证:![]() .
.
【答案】(1) ![]() ;(2)见解析
;(2)见解析
【解析】
(1)过点B作BM⊥AD于点G,根据等边三角形的性质,求出AM=3,BM=![]() 在Rt△AMB中,根据
在Rt△AMB中,根据![]() ,求出MD的长度,即可求出线段AD的长;
,求出MD的长度,即可求出线段AD的长;
(2)延长AF至点N使得FN=AF,连接BN,先证明出△ADF≌△NBF,得出DA=BN,∠DAF=∠N,进而得出∠N=∠E,再用AAS判断出△ABN≌△ACE即可得出结论;
(1) 过点B作BM⊥AD于点G
∵△ABC是等边三角形,
∴AM=3,BM=![]()
在Rt△AMB中,![]()
∴MD=![]()
∴AD=AM+MD=![]()

(2) 延长AF至点N使得FN=AF,连接BN

∵ F是BD的中点
∴BF=DF
在△ADF和△NBF中:
 ,
,
∴△ADF≌△NBF(SAS),
∴DA=BN,∠DAF=∠N
∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠ACB=60°
∵∠EAF=60°,
∴∠BAF=∠DAE
∵∠EAF=∠EAC+∠DAF=60°,∠ACD=∠EAC+∠E=60°,
∴∠DAF=∠E,
∴∠N=∠E
在△ABN和△ACE中:
 ,
,
∴△ABN≌△ACE(AAS),∴BN=CE,∴AD=DC,∴BD⊥AC,∴BD=![]()

练习册系列答案
相关题目