Question

【题目】如图，在等腰△ABC中，AB＝BC，点D是AC边的中点，延长BD至点E，使得DE＝BD，连结CE．

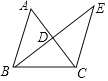
（1）求证：△ABD≌△CED．

（2）当BC＝5，CD＝3时，求△BCE的周长．

Answer 1

【答案】（1）见解析；（2）△BCE的周长为18．

【解析】

（1）利用全等三角形的判定定理SAS证得结论；

（2）利用勾股定理求得BD＝4，然后利用三角形的周长公式解答．

（1）证明：∵AB＝BC，点D是AC边的中点，

∴AD＝CD，∠ADB＝∠CDE＝90°．

又∵DE＝BD，

∴△ABD≌△CED（SAS）；

（2）解：∵BD＝＝＝4，

∴BE＝2BD＝8．

又∵CE＝AB＝BC＝5，

∴BC+CE+BE＝5+5+8＝18，即△BCE的周长为18．