Question

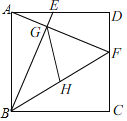
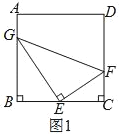
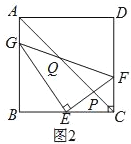
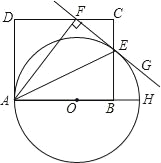
【题目】如图，AH是圆O的直径，AE平分∠FAH，交⊙O于点E，过点E的直线FG⊥AF，垂足为F，B为直径OH上一点，点E、F分别在矩形ABCD的边BC和CD上．

（1）求证：直线FG是⊙O的切线；

（2）若AD=8，EB=5，求⊙O的直径．

Answer 1

【答案】（1）见解析；（2）⊙O的直径为．

【解析】

（1）连接OE，证明FG是⊙O的切线，只要证明∠OEF=90°即可；

（2）先求出CE，利用角平分线得出EF=BE=5，进而求出CF，即可利用勾股定理求出AB，最后用勾股定理即可得出结论．

（1）如图1，连接OE，

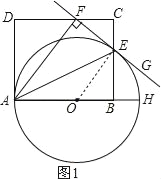
∵OA=OE，

∴∠EAO=∠AEO，

∵AE平分∠FAH，

∴∠EAO=∠FAE，

∴∠FAE=∠AEO，

∴AF∥OE，

∴∠AFE+∠OEF=180°，

∵AF⊥GF，

∴∠AFE=∠OEF=90°，

∴OE⊥GF，

∵点E在圆上，OE是半径，

∴GF是⊙O的切线．

（2）设AB=x，

∵四边形ABCD是矩形，

∴AB=CD=x，BC=AD=8，

∴CE=BC﹣BE=3，

∵AE是∠BAF的角平分线，BE⊥AB，EF⊥AF，

∴EF=BE=5，

在Rt△CEF中，根据勾股定理得，CF=4，

∴DF=CD﹣CF=x﹣4，

在Rt△ABE和Rt△AFE中， ，

∴Rt△ABE≌Rt△AFE（HL），

∴AF=AB=x，

在Rt△ADF中，x2﹣（x﹣4）2=64，

∴x=10，

∴AB=10，

设⊙O的半径为r，

∴OB=10﹣r，

在Rt△BOE中，r2﹣（10﹣r）2=25，

∴r= ，

∴⊙O的直径为．