题目内容
【题目】如图①,已知线段 AB=12cm,点 C 为 AB 上的一个动点,点 D,E 分别是 AC 和 BC的中点.
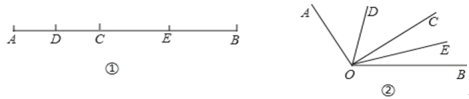
(1)若 AC=4cm,求 DE 的长.
(2)若 AC=acm(不超过 12cm),求 DE 的长.
(3)知识迁移:如图②,已知∠AOB=120°,过角的内部任意一点 C 画射线OC,若OD,OE 分别平分∠AOC 和∠BOC,求∠DOE 的度数.
【答案】(1)6
(2)6
(3)60°
【解析】
(1)由AB=12cm,AC=4cm,即可推出BC=8cm,然后根据点 D,E 分别是 AC 和 BC的中点,即可推出CD=2cm,CE=4cm,即可推出DE的长度.
(2)由AC=acm,可知BC=AB-AC=12-a,再根据点 D,E 分别是 AC 和 BC的中点,可推出DE=CD+CE=![]() (AC+BC),即可求解.
(AC+BC),即可求解.
(3)由OD,OE 分别平分∠AOC 和∠BOC,可推出![]() ,即可求解.
,即可求解.
(1)∵AB=12cm,AC=4cm,
∴BC=8cm,
∵点 D,E 分别是 AC 和 BC的中点,
∴CD=2cm,CE=4cm,
∴DE=6cm.
(2)∵AC=acm,
∴BC=AB-AC=12-a,
∵点 D,E 分别是 AC 和 BC的中点,
∴DE=CD+CE=![]() (AC+BC)=
(AC+BC)=![]() (a+12-a) =6cm,
(a+12-a) =6cm,
(3)∵OD,OE 分别平分∠AOC 和∠BOC,
∴![]()
∵∠AOB=120°,
∴![]() 60°.
60°.

【题目】观察如图图形,把一个三角形分别连接其三边中点,构成4个小三角形,挖去中间的一个小三角形(如图1),对剩下的三个小三角形再分别重复以上做法,……,据此解答下面的问题
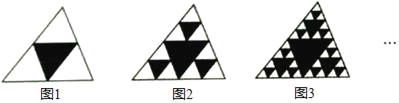
(1)填写下表:
图形 | 挖去三角形的个数 |
图形1 | 1 |
图形2 | 1+3 |
图形3 | 1+3+9 |
图形4 |
|
(2)根据这个规律,求图n中挖去三角形的个数wn;(用含n的代数式表示)
(3)若图n+1中挖去三角形的个数为wn+1,求wn+1﹣Wn