题目内容
如图，在△ABC中，∠C=90°，AB的垂直平分线DE交AC于点D，交AB于点E，若BC=3，AB=5，则BD=考点：线段垂直平分线的性质
专题：
分析：根据题意可知，在Rt△ABC中，∠C=90°，AB=5，BC=3，根据勾股定理可得AC的长度，AC=4，设CD为x，则AD=4-x，在Rt△CDB中，CD=AD=4-x，BC=3，再一次使用勾股定理可解出x，再根据勾股定理求出BD即可．
解答：解：在Rt△ABC中，∠C=90°，AB=5，BC=3，
∴AC=4，
又∵AB的垂直平分线DE交边AC于点D，
∴BD=AD，设CD=x，则BD=AD=4-x，BC=3，
在Rt△BCD中，（4-x）2=x2+32，
解之x=
，
即CD=
，
由勾股定理得：BD=
=
=
，
故答案为：
．
∴AC=4，
又∵AB的垂直平分线DE交边AC于点D，
∴BD=AD，设CD=x，则BD=AD=4-x，BC=3，
在Rt△BCD中，（4-x）2=x2+32，
解之x=
| 7 |
| 8 |
即CD=
| 7 |
| 8 |
由勾股定理得：BD=
| BC2+CD2 |
(
|
| 25 |
| 8 |
故答案为：
| 25 |
| 8 |
点评：此题主要考查了直角三角形的有关知识和垂直平分线的性质及勾股定理的灵活运用，主要考查学生的计算能力．
练习册系列答案
阅读快车系列答案
相关题目
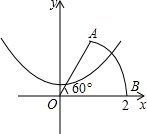如图，以扇形OAB的顶点O为原点，半径OB所在的直线为x轴，建立平面直角坐标系，点B的坐标为（2，0），扇形的圆心角是60°，若抛物线y=x2+k与扇形OAB的边界总有两个公共点，则实数取值范围是抛物线y=4x2与y=-2x2的图象，开口较大的是（ ）
| A、y=-2x2 |
| B、y=4x2 |
| C、同样大 |
| D、无法确定 |