题目内容
4(x+1)2-7(x-1)(x+1)+3(1-x)2,其中(x+
)2=0.
| 1 | 2 |
分析:根据非负数的性质求出x的值,再把要求的式子用十字相乘法进行因式分解,然后代值计算即可.
解答:解:∵(x+
)2=0,
∴x=-
,
∴4(x+1)2-7(x-1)(x+1)+3(1-x)2=4(x+1)2-7(x-1)(x+1)+3(x-1)2
=[(x+1)-(x-1)][4(x+1)-3(x-1)]
=2(x+7)2x+14
=2×(-
)+14
=13.
| 1 |
| 2 |
∴x=-
| 1 |
| 2 |
∴4(x+1)2-7(x-1)(x+1)+3(1-x)2=4(x+1)2-7(x-1)(x+1)+3(x-1)2
=[(x+1)-(x-1)][4(x+1)-3(x-1)]
=2(x+7)2x+14
=2×(-
| 1 |
| 2 |
=13.
点评:此题考查了因式分解的应用,用到的知识点是十字相乘进行因式分解,非负数的性质,关键是用十字相乘法把要求的式子进行化简.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案
相关题目
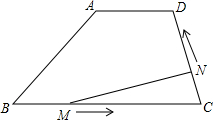 每秒2个单位长度的速度向终点A运动,若M、N两点同时出发,当其中一点到达端点(终点)时,另一点也随之停止运动,设运动时间为t秒.
每秒2个单位长度的速度向终点A运动,若M、N两点同时出发,当其中一点到达端点(终点)时,另一点也随之停止运动,设运动时间为t秒.