题目内容
(本小题满分5分)在△ABC中,AB=AC,∠BAC=120°,过点C作CD∥AB,且CD=2AB,联结BD,BD=2.求△ABC的面积.
解:过点B作BE⊥AC交CD于E,过点A作AF⊥CB于F

∵CD∥AB,AB=AC,
∴四边形ABEC是菱形---------------------------------------1分
∴BE=CE=AB
∵∠BAC=120°
∴∠ABC=30°,∠ABE=60°,∠BED=60°
∵CD=2AB,BD=2
∴△ABC是等边三角形,AB="2 " --------------------------------------------------------------------2分
在△ABF中,∠AFB=90°, ∠ABC=30°,AB ="2"
∴BF= ,AF="1 " ---------------------------------------------------------------------------3分
,AF="1 " ---------------------------------------------------------------------------3分
∴BC=2 -------------------------------------------------------------------------------4分
-------------------------------------------------------------------------------4分
∴△ABC的面积为 -------------------------------------------------------------------------------5分解析:
-------------------------------------------------------------------------------5分解析:
略

∵CD∥AB,AB=AC,
∴四边形ABEC是菱形---------------------------------------1分
∴BE=CE=AB
∵∠BAC=120°
∴∠ABC=30°,∠ABE=60°,∠BED=60°
∵CD=2AB,BD=2
∴△ABC是等边三角形,AB="2 " --------------------------------------------------------------------2分
在△ABF中,∠AFB=90°, ∠ABC=30°,AB ="2"
∴BF=
 ,AF="1 " ---------------------------------------------------------------------------3分
,AF="1 " ---------------------------------------------------------------------------3分∴BC=2
 -------------------------------------------------------------------------------4分
-------------------------------------------------------------------------------4分∴△ABC的面积为
 -------------------------------------------------------------------------------5分解析:
-------------------------------------------------------------------------------5分解析:略

练习册系列答案
相关题目
 (
(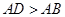 )中,将纸片折叠一次,使点
)中,将纸片折叠一次,使点 与
与 重合,再展开,折痕
重合,再展开,折痕 交
交 边于
边于 ,交
,交 边于
边于 ,分别连结
,分别连结 和
和 .
.
 是菱形;
是菱形; 交
交 于
于 ,求证:
,求证:
 ,
, 的面积为
的面积为 ,求
,求
 为半径的圆的内部的概率.
为半径的圆的内部的概率. 图象上,过点B作BD⊥x轴,垂足为D,且B点横坐标为-3.
图象上,过点B作BD⊥x轴,垂足为D,且B点横坐标为-3.