题目内容
 如图△ABC的面积为a.
如图△ABC的面积为a.
(1)如图1,延长△ABC的边BC到点D,使CD=BC,连接DA.则△ACD的面积为______(用含a的代数式表示);
(2)如图2,延长△ABC的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连接DE,BE.则阴影部分的面积为______(用含a的代数式表示).
 解:(1)如图,过点A作AM⊥BC于M,
解:(1)如图,过点A作AM⊥BC于M,则△ABC的面积=
 BC•AM=a,
BC•AM=a,∵CD=BC,
∴△ACD的面积=
 CD•AM=
CD•AM= BC•AM=a;
BC•AM=a;(2)连接AD,
∵CD=BC,
∴S△ACD=S△ABC=a,
∵AE=CA,
∴S△ABE=S△ABC=a,
S△ADE=S△ACD=a,
∴阴影部分的面积=S△ACD+S△ABE+S△ADE=a+a+a=3a.
故答案为:a;3a.
分析:(1)过点A作AM⊥BC于M,然后根据三角形的面积公式列式计算即可得解;
(2)连接AD,根据等底等高的三角形的面积相等解答.
点评:本题考查了三角形的面积,主要是等底等高的三角形的面积相等的证明与应用,(2)把阴影部分分成三个三角形是解题的关键.

练习册系列答案
相关题目
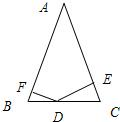 已知如图△ABC的面积为16,AB=AC=8,D是BC上任意一点,过D作DE⊥AC,DF⊥AB,垂足为E,F,若DF=x,DE=y,y关于x的函数关系式是
已知如图△ABC的面积为16,AB=AC=8,D是BC上任意一点,过D作DE⊥AC,DF⊥AB,垂足为E,F,若DF=x,DE=y,y关于x的函数关系式是 如图△ABC的面积为a.
如图△ABC的面积为a.
 已知如图△ABC的面积为16,AB=AC=8,D是BC上任意一点,过D作DE⊥AC,DF⊥AB,垂足为E,F,若DF=x,DE=y,y关于x的函数关系式是________.
已知如图△ABC的面积为16,AB=AC=8,D是BC上任意一点,过D作DE⊥AC,DF⊥AB,垂足为E,F,若DF=x,DE=y,y关于x的函数关系式是________.