题目内容
7.计算:(1)$\frac{{4{a^4}{b^2}}}{{5{c^3}}}÷\frac{{8{a^2}{b^2}}}{{15{c^2}}}$
(2)$(\frac{x}{x+2}-\frac{4}{{{x^2}+2x}})•\frac{x}{x+1}$.
分析 (1)将分式的除法转化为乘法,然后化简即可;
(2)先选括号里面的再根据分式的乘法进行化简即可.
解答 解:(1)$\frac{{4{a^4}{b^2}}}{{5{c^3}}}÷\frac{{8{a^2}{b^2}}}{{15{c^2}}}$
=$\frac{4{a}^{4}{b}^{2}}{5{c}^{3}}×\frac{15{c}^{2}}{8{a}^{2}{b}^{2}}$
=$\frac{3{a}^{2}}{2c}$;
(2)$(\frac{x}{x+2}-\frac{4}{{{x^2}+2x}})•\frac{x}{x+1}$
=$\frac{{x}^{2}-4}{x(x+2)}•\frac{x}{x+1}$
=$\frac{(x+2)(x-2)}{x(x+2)}•\frac{x}{x+1}$
=$\frac{x-2}{x+1}$.
点评 本题考查分式的混合运算,解题的关键是明确分式混合运算的计算方法.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
18.计算(-1)2016结果正确的是( )
| A. | -1 | B. | 1 | C. | -2016 | D. | 2016 |
15.在下列分解因式的过程中,分解因式正确的是( )
| A. | -xz+yz=-z(x+y) | B. | 3a2b-2ab2+ab=ab(3a-2b) | ||
| C. | 6xy2-8y3=2y2(3x-4y) | D. | x2+3x-4=(x+2)(x-2)+3x |

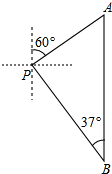 如图,小明从P处出发,沿北偏东60°方向行驶200米到达A处,接着向正南方向行驶一段时间到达B处.在B处观测到出发时所在的P处在北偏西37°方向上,这时P、B两点相距多少米?(精确到1米,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,
如图,小明从P处出发,沿北偏东60°方向行驶200米到达A处,接着向正南方向行驶一段时间到达B处.在B处观测到出发时所在的P处在北偏西37°方向上,这时P、B两点相距多少米?(精确到1米,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,