题目内容
(1)观察与猜想:已知当0°<α<60°时,下列关系式有且只有一个正确,正确的是______(填代号)A.2sin(30°+α)=sinα+
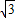
B.2sin(30°+α)=2sinα+
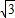
C.2sin(30°+α)=
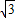 sinα+cosα.
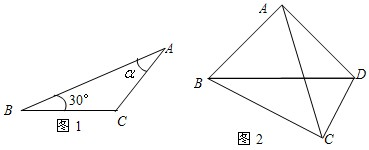
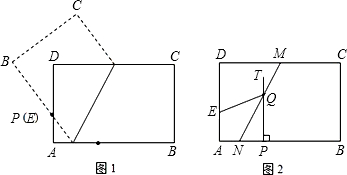
sinα+cosα.(2)探究与证明:如图1,△ABC中,∠A=α,∠B=30°,AC=1,请利用图1证明(1)中你猜想的结论;
(3)应用新知识解决问题:
两块分别含有45°和30°的直角三角板如图2方式摆放在同一平面内,BD=8
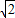 ,求S△ABC.
,求S△ABC.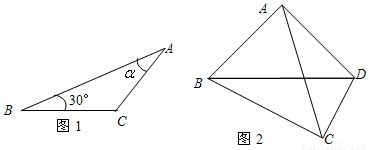
【答案】分析:(1)正确的选项为C;
(2)过A作AD⊥BM,交BC延长线于点M,过C作CE⊥AB,在直角三角形ABM中,利用30°所对的直角边等于斜边的一半,得到AM等于AB的一半,再由∠ACM为三角形ABC的外角,利用外角性质得到∠ACM=30°+α,在直角三角形AEC中,表示出EC与AE,在直角三角形BEC中,表示出BE,由AE+EB表示出AB,化简后即可得证;
(3)由上述结论2sin(30°+45°)=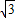 sin45°+cos45°,求出sin75°的值,过A作AE垂直于BC,由BD分别求出AB与BC的长,在直角三角形AB中,利用锐角三角函数定义求出AE的长,利用三角形的面积公式即可求出三角形ABC的面积.
sin45°+cos45°,求出sin75°的值,过A作AE垂直于BC,由BD分别求出AB与BC的长,在直角三角形AB中,利用锐角三角函数定义求出AE的长,利用三角形的面积公式即可求出三角形ABC的面积.
解答: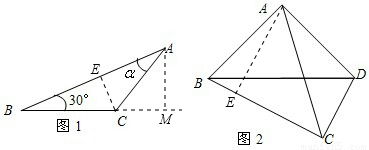 解:(1)正确的选项为C;
解:(1)正确的选项为C;
(2)过A作AM⊥BM,交BC延长线于点M,过C作CE⊥AB,
∵∠AMB=90°,∠B=30°,
∴AM= AB,即AB=2AM,
AB,即AB=2AM,
∵∠ACM为△ABC的外角,
∴∠ACM=∠B+∠BAC=30°+α,
在Rt△ACM中,AC=1,
∴AM=ACsin∠ACM=sin(30°+α),
则AB=2sin(30°+α),
在Rt△AEC中,EC=ACsinα=sinα,AE=ACcosα=cosα,
在Rt△BEC中,BE= =
=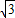 CE=
CE=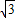 sinα,
sinα,
则AB=BE+AE=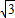 sinα+cosα,
sinα+cosα,
则2sin(30°+α)=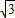 sinα+cosα;
sinα+cosα;
(3)∵∠ABD=45°,∠CBD=30°,
∴2sin(30°+45°)=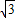 sin45°+cos45°=
sin45°+cos45°=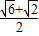 ,
,
∴sin75°=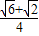 ,
,
过A作AE⊥BC,
在等腰直角三角形ABD中,BD=8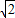 ,
,
∴AB=AD=8,
在Rt△BCD中,BD=8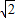 ,
,
∴CD=4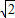 ,BC=
,BC=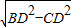 =4
=4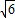 ,
,
在Rt△ABE中,sin75°=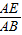 ,
,
∴AE=8×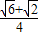 =2
=2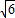 +2
+2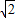 ,
,
则S△ABC= BC•AE=
BC•AE= ×4
×4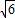 ×(2
×(2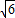 +2
+2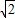 )=24+8
)=24+8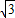 .
.
点评:此题属于解直角三角形题型,涉及的知识有:含30°直角三角形的性质,锐角三角函数定义,勾股定理,以及特殊角的三角函数值,熟练性质及定理是解本题的关键.
(2)过A作AD⊥BM,交BC延长线于点M,过C作CE⊥AB,在直角三角形ABM中,利用30°所对的直角边等于斜边的一半,得到AM等于AB的一半,再由∠ACM为三角形ABC的外角,利用外角性质得到∠ACM=30°+α,在直角三角形AEC中,表示出EC与AE,在直角三角形BEC中,表示出BE,由AE+EB表示出AB,化简后即可得证;
(3)由上述结论2sin(30°+45°)=
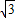 sin45°+cos45°,求出sin75°的值,过A作AE垂直于BC,由BD分别求出AB与BC的长,在直角三角形AB中,利用锐角三角函数定义求出AE的长,利用三角形的面积公式即可求出三角形ABC的面积.
sin45°+cos45°,求出sin75°的值,过A作AE垂直于BC,由BD分别求出AB与BC的长,在直角三角形AB中,利用锐角三角函数定义求出AE的长,利用三角形的面积公式即可求出三角形ABC的面积.解答:
 解:(1)正确的选项为C;
解:(1)正确的选项为C;(2)过A作AM⊥BM,交BC延长线于点M,过C作CE⊥AB,
∵∠AMB=90°,∠B=30°,
∴AM=
 AB,即AB=2AM,
AB,即AB=2AM,∵∠ACM为△ABC的外角,
∴∠ACM=∠B+∠BAC=30°+α,
在Rt△ACM中,AC=1,
∴AM=ACsin∠ACM=sin(30°+α),
则AB=2sin(30°+α),
在Rt△AEC中,EC=ACsinα=sinα,AE=ACcosα=cosα,
在Rt△BEC中,BE=
 =
=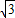 CE=
CE=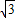 sinα,
sinα,则AB=BE+AE=
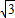 sinα+cosα,
sinα+cosα,则2sin(30°+α)=
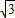 sinα+cosα;
sinα+cosα;(3)∵∠ABD=45°,∠CBD=30°,
∴2sin(30°+45°)=
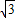 sin45°+cos45°=
sin45°+cos45°=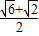 ,
,∴sin75°=
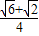 ,
,过A作AE⊥BC,
在等腰直角三角形ABD中,BD=8
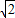 ,
,∴AB=AD=8,
在Rt△BCD中,BD=8
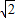 ,
,∴CD=4
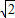 ,BC=
,BC=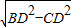 =4
=4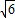 ,
,在Rt△ABE中,sin75°=
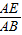 ,
,∴AE=8×
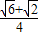 =2
=2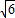 +2
+2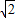 ,
,则S△ABC=
 BC•AE=
BC•AE= ×4
×4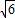 ×(2
×(2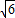 +2
+2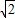 )=24+8
)=24+8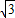 .
.点评:此题属于解直角三角形题型,涉及的知识有:含30°直角三角形的性质,锐角三角函数定义,勾股定理,以及特殊角的三角函数值,熟练性质及定理是解本题的关键.

练习册系列答案
相关题目
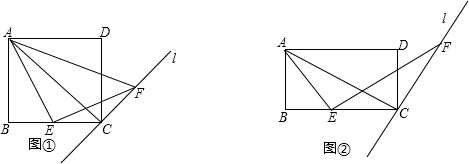


 ,求S△ABC.
,求S△ABC.