题目内容
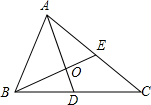△ABC的两条中线AD、BE交于点O，则AO：OD=________．
2：1
分析：根据三角重心的定义得出O就是△ABC的重心，再根据重心到顶点的距离与重心到对边中点的距离之比为2：1，即可得出答案．
解答：∵AD、BE是△ABC的中线，交点为O，
∴O为△ABC的重心，
∵重心到顶点的距离与重心到对边中点的距离之比为2：1，
∴AO：OD=2：1，；
故答案为：2：1．
点评：本题主要考查了三角形重心，掌握三角形的重心到顶点的距离是它到对边中点的距离的2倍是解决问题的关键，是一道基础题．
分析：根据三角重心的定义得出O就是△ABC的重心，再根据重心到顶点的距离与重心到对边中点的距离之比为2：1，即可得出答案．
解答：∵AD、BE是△ABC的中线，交点为O，
∴O为△ABC的重心，
∵重心到顶点的距离与重心到对边中点的距离之比为2：1，
∴AO：OD=2：1，；
故答案为：2：1．
点评：本题主要考查了三角形重心，掌握三角形的重心到顶点的距离是它到对边中点的距离的2倍是解决问题的关键，是一道基础题．
练习册系列答案
相关题目
10、如图，△ABC的两条中线AD、BE相交于点G，如果AD=3，那么GD=
9、如图所示，AD和BE是△ABC的两条中线，相交于点O，设△AOB和四边形CDOE的面积分别为S1、S2，则S1和S2的关系为（ ）
如图，已知△ABC的两条中线AD，BE相交于点F，得到8个图形：△ABD，△ACD，△BAE，△BCE，△FAB，△FAE，△FBD，四边形CEFD，现从中任取两个图形，求取得的这两个图形面积相等的概率．
（2012•集美区一模）如图△ABC的两条中线AD与BE相交于G，EF∥AD，EF交BC于F，已知：AG=4厘米，则DG=
如图，在△ABC中，AB=AC，△ABC的两条中线BD、CE交于O点，