Question

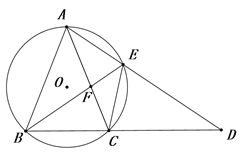
【题目】已知点O在内部，连接OA，OB，OC，说明：．

Answer 1

【答案】证明见解析

【解析】

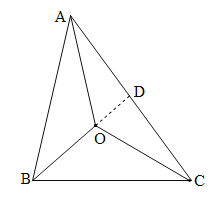
延长BO交AC于D．在△AOB、△BOC、△AOC中，由三角形三边关系定理列式，三式相加可得2(OA+OB+OC)＞AB+BC+AC，即可证明不等式左边部分成立．在△ADO、△BDC中，由三角形三边关系定理列式，两式相加可得OA+BO＜AC+BC，同理可得：OC+OB＜AB+AC，OC+OA＜AB+BC，三式相加即可证明不等式右边部分成立．

延长BO交AC于D．

在中，，①

在中，②

在中，，③

①＋②＋③得．

即．

在△ADO中，OA＜AD+OD，

在△BDC中，BD＜DC+BC，

∴OA+BD＜AD+OD+DC+BC，

即OA+BO+OD＜AC+OD+BC，

∴OA+BO＜AC+BC ④

同理： ⑤

，⑥

④＋⑤＋⑥得，

即．

∴．