题目内容
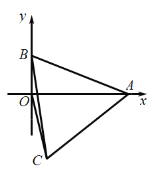
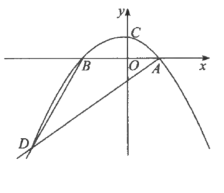
【题目】如图,在平面直角坐标系中,抛物线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,且经过点
,且经过点![]() ,连接
,连接![]() .
.
(1)求该抛物线的函数关系式;
(2)△ANM与![]() 是否相似?若相似,请求出此时点
是否相似?若相似,请求出此时点![]() 、点
、点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)若点![]() 是直线
是直线![]() 上方的抛物线上一动点(不与点
上方的抛物线上一动点(不与点![]() 重合),过
重合),过![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,以
,以![]() 为直径作⊙
为直径作⊙![]() ,则⊙
,则⊙![]() 在直线
在直线![]() 上所截得的线段长度的最大值等于 .(直接写出答案)
上所截得的线段长度的最大值等于 .(直接写出答案)
【答案】(1)![]() ;(2)点M(0,
;(2)点M(0,![]() )、点N(
)、点N(![]() ,0)或点M(0,
,0)或点M(0,![]() ),N(-3,0)或点M(-1,
),N(-3,0)或点M(-1,![]() )、点N(-3,0)或N(
)、点N(-3,0)或N(![]() ,0)、M(-1,
,0)、M(-1,![]() );(3)QH有最大值,当x=
);(3)QH有最大值,当x=![]() 时,其最大值为
时,其最大值为![]() .
.
【解析】
(1)用交点式函数表达式得:y=a(x-2)(x+3),将点D坐标代入上式即可求解;
(2)分∠MAB=∠BAD、∠MAB=∠BDA,两种大情况、四种小情况,分别求解即可;
(3)根据题意,利用二次函数的性质和三角函数,QH=PQcos∠PQH=![]() PQ=
PQ=![]()
![]()
![]() =
=![]() ,即可求解.
,即可求解.
解:(1)用交点式函数表达式得:y=a(x-2)(x+3),
将点D坐标代入上式并解得:![]() ,
,
故函数的表达式为:![]() …①,
…①,
则点C(0,![]() );
);
(2)由题意得:AB=5,AD=10,BD=![]() ,
,
①∠MAN=∠ABD时,
(Ⅰ)当△ANM∽△ABD时,
直线AD所在直线的k值为![]() ,则直线AM表达式中的k值为
,则直线AM表达式中的k值为![]() ,
,
则直线AM的表达式为:![]() ,故点M(0,
,故点M(0,![]() ),
),![]() ,则AN=
,则AN=![]() ,则点N(
,则点N(![]() ,0);
,0);
(Ⅱ)当△AMN∽△ABD时,
同理可得:点N(-3,0),点M(0,![]() ),
),
故点M(0,![]() )、点N(
)、点N(![]() ,0)或点M(0,
,0)或点M(0,![]() ),N(-3,0);
),N(-3,0);
②∠MAN=∠BDA时,
(Ⅰ)△ABD∽△NMA时,
∵AD∥MN,则tan∠MAN=tan∠BDA=![]() ,
,
AM:y=![]() (x-2),则点M(-1,
(x-2),则点M(-1,![]() )、点N(-3,0);
)、点N(-3,0);
(Ⅱ)当△ABD∽△MNA时,![]() ,即
,即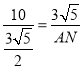 ,
,
解得:AN=![]() ,
,
故点N(![]() ,0)、M(-1,
,0)、M(-1,![]() );
);
故:点M(-1,![]() )、点N(-3,0)或N(
)、点N(-3,0)或N(![]() ,0)、M(-1,
,0)、M(-1,![]() );
);
综上,点M(0,![]() )、点N(
)、点N(![]() ,0)或点M(0,
,0)或点M(0,![]() ),N(-3,0)或点M(-1,
),N(-3,0)或点M(-1,![]() )、点N(-3,0)或N(
)、点N(-3,0)或N(![]() ,0)、M(-1,
,0)、M(-1,![]() );
);
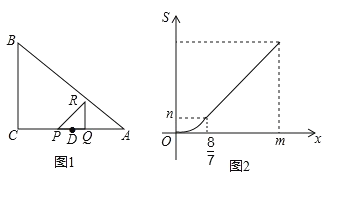
(3)如图所示,连接PH,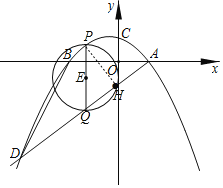
由题意得:tan∠PQH=![]() ,则cos∠PQH=
,则cos∠PQH=![]() ,
,
则直线AD的表达式为:y=![]() ,
,
设点P(x,![]() ),则点Q(x,
),则点Q(x,![]() ),
),
则QH=PQcos∠PQH=![]() PQ=
PQ=![]()
![]()
![]()
=![]()
=![]() ,
,
∵![]() ,
,
故QH有最大值,当x=![]() 时,其最大值为
时,其最大值为![]() .
.