题目内容
如图，AD∥BC，∠1=∠2，∠3=∠4，AD=4，BC=2，那么AB=________．
6
分析：作辅助线延长AD，BE交于F，已知∠1=∠2，∠3=∠4，可得CE=DE，BC=DF，即可求解．
解答：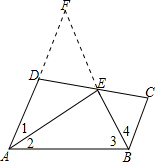
解：延长AD，BE交于F．
∵AD∥BC，∠4=∠F=∠3，
∴AB=AF，
∵∠1=∠2，AE⊥BF，BE=EF，AD∥BC，
∴CE=DE，BC=DF，
∴AF=AD+DF=AD+BC=6，
AB=AF=6．
故答案为6．
点评：本题考查了梯形和三角形的中位线性质，难度不大，关键熟练灵活运用中位线定理．
分析：作辅助线延长AD，BE交于F，已知∠1=∠2，∠3=∠4，可得CE=DE，BC=DF，即可求解．
解答：
解：延长AD，BE交于F．∵AD∥BC，∠4=∠F=∠3，
∴AB=AF，
∵∠1=∠2，AE⊥BF，BE=EF，AD∥BC，
∴CE=DE，BC=DF，
∴AF=AD+DF=AD+BC=6，
AB=AF=6．
故答案为6．
点评：本题考查了梯形和三角形的中位线性质，难度不大，关键熟练灵活运用中位线定理．
练习册系列答案
相关题目
2、如图，AD∥BC，则下列式子成立的是（ ）
8、如图：AD∥BC，AB=AC，∠BAC=80°，则∠DAC=
4、如图，AD⊥BC，DE∥AB，则∠CDE与∠BAD的关系是（ ）
已知如图，AD=BC，要得到△ABD≌△CDB，可以添加角的条件：∠
已知：如图，AD⊥BC，EF⊥BC，∠1=∠2．求证：AB∥GF．