题目内容
先阅读,再解题:因为1-
| 1 |
| 2 |
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2×3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 3×4 |
所以
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 49×50 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 49 |
| 1 |
| 50 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 49 |
| 1 |
| 50 |
| 1 |
| 50 |
| 49 |
| 50 |
参照上述解法计算:
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| 5×7 |
| 1 |
| 49×51 |
分析:根据题中给出的材料可知利用通分的逆运算把分式拆成两个分数的加法或减法的形式,可使计算简便.
解答:解:原式=
(1-
+
-
+
-
+…+
-
)=
(1-
)=
×
=
.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 49 |
| 1 |
| 51 |
| 1 |
| 2 |
| 1 |
| 51 |
| 1 |
| 2 |
| 50 |
| 51 |
| 25 |
| 51 |
点评:解此类题目的关键是熟悉分数的通分方法,利用通分的逆运算把分式拆成两个分数的加法或减法的形式,可使计算简便.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
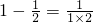 ,
, ,
,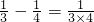 ,…
,… =
=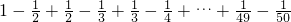 =
=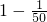 =
=
 .
.