题目内容

先阅读，再解题：
因为1-
1
2
=
1
1×2
，
1
2
-
1
3
=
1
2×3
，
1
3
-
1
4
=
1
3×4
，…所以
1
1×2
+
1
2×3
+
1
3×4
+…+
1
49×50
=(1-
1
2
)+(
1
2
-
1
3
)+(
1
3
-
1
4
)+…+(
1
49
-
1
50
)=1-
1
2
+
1
2
-
1
3
+
1
3
-
1
4
+…+
1
49
-
1
50
=1-
1
50
．=
49
50

参照上述解法计算：
2013
1×3
+
2013
3×5
+
2013
5×7
+…+
2013
2011×2013
．
分析：观察已知等式得到拆项规律，原式变形后计算即可得到结果．
解答：解：根据题意得：
原式=2013×
1
2
×（1-
1
3
+
1
3
-
1
5
+…+
1
2011
-
1
2013
）
=2013×
1
2
×
2012
2013

=1006．
点评：此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
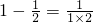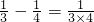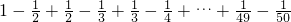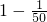先阅读，再解题：
因为1-
1
2
=
1
1×2
，
1
2
-
1
3
=
1
2×3
，
1
3
-
1
4
=
1
3×4
，…
所以
1
1×2
+
1
2×3
+
1
3×4
+…+
1
49×50
=(1-
1
2
)+(
1
2
-
1
3
)+(
1
3
-
1
4
)+…+(
1
49
-
1
50
)=1-
1
2
+
1
2
-
1
3
+
1
3
-
1
4
+…+
1
49
-
1
50
=1-
1
50
=
49
50

参照上述解法计算：
1
1×3
+
1
3×5
+
1
5×7
+…+
1
49×51
．

先阅读，再解题：

因为，，，……

所以

参照上述解法计算：

先阅读，再解题：
因为数学公式，数学公式，数学公式，…
所以数学公式=数学公式=数学公式=数学公式
参照上述解法计算：数学公式．
先阅读，再解题：
因为1-
1
2
=
1
1×2
，
1
2
-
1
3
=
1
2×3
，
1
3
-
1
4
=
1
3×4
，…
所以
1
1×2
+
1
2×3
+
1
3×4
+…+
1
49×50
=(1-
1
2
)+(
1
2
-
1
3
)+(
1
3
-
1
4
)+…+(
1
49
-
1
50
)=1-
1
2
+
1
2
-
1
3
+
1
3
-
1
4
+…+
1
49
-
1
50
=1-
1
50
=
49
50

参照上述解法计算：
1
1×3
+
1
3×5
+
1
5×7
+…+
1
49×51
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网